《高等数学》课程教学资源（课件讲稿）第四章_不定积分练习题及参考答案15道

不定积分练习题dxdx2x-13.2.1dx;(x+1(x-2)simxcosxarctgxdx5.6.4.sin5xsin7xdx;dx;/x(1+x)x+vi-x8. Jcos(m x)dx;7.[xarctgxdx;9.sinxdx;W12.Jeax;11. Jxcos' xdk;10.dx;21++8xernX13.15.14.sinxcosxdx;dx;dx;+1O

dx分子分母同除以1.凑微分cos2(x)sinxcosxdltgxsec=n(tga)+C解：原式=tgxtgx2x-12xdx微2.dx分1-x-dx1-x-2-x-arcsinx+C解：原式=3dx3.裂项x+1(x-2)1（)[n(x+1)-m(x-2)]+c解：=-+Cdbx32

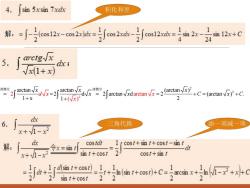
4.sin5xsin7xdx积化和差11(cos12x-cos2x)dx=cos2xdx-cos12xdx解：sin12r+Csin2424Aarctgyx5.dx;/x(1+ x)凑微分d/x*”2 arctan Vxdarctan x=2 (arctan Va) arctan Vx d Jx=2]arctanyx装微+C=(arctan Vx)+C=2(/x)1+xdxV6.三角代换添一项减一项x+/1-x?dxcostdtrcost+sint+cost-sint解：令x=sindt2sin t+costcost+sintx+111sint+costat+!2+x+(sint+cost)+C=-arcsinx+-h-hn-22222sint+cost

2 2 a 2 rctan arctan (arctan ) 2 2 d 2 arc arctan ( ) tan d 2 (arctan ) . 1 x 1 2 x x x d x x x x    x  C  x C      凑微分 凑微分

7.Jxarctgxdx凑微分分部积分解：原式-,Jarctgde)-(arctgr-jx1+amg-a+are=m(1+x)+c66x3=x(1+x)-x8. Jcos(n x)dx分部积分解：原式=xcos(ln x)+xsin(lnx)-dx=xcos(lnx)+sin(lnx)dxX=xcos(lmx)+xsin(mx)-xdsim (lnx)=xcosx(lnx)+xsin(nx)-cos(lnx)a分部积分原式美xcosx(lnx)+sin(lnx)]+C故[cos(ln x)dx=-2

分部积分 分部积分 原式

9.Jsinxcx换元解：令/x=t，则x=t，d=3tdt分部积分原式=sint3t'dt=-3t'dcost=-3t?cost+3cost.2tdt=-3f.cost+6tdsin t=-3t cost+6tsint-6sintdt=-3t°cost+6tsint+6cost+C=-3xcos/x+6/xsin/x+6cos/x+C10.dbx换元换元rsectdtdui解：原式令u=tgt=今1+,84secat142sec(t)=111/cos(t)costdt=(1+cos2t)dt=一sin 2t+C.8161111ZXf0+Carctgu-ar'ctg-8881+8(1+xVi+u?

换元 分部积分 换元 换元

11.[xcosxcx倍角公式微分解：原式=[ (]-[a+ 02x]-→+[ dm2)211卫-I元xsin 2x-sin 2xdx==xsin2x+=cos2x+C484444分部积分Tedx12.换元分部积分解：令x=t，则x=t，d=3tdt原式-Je'3t’dt=3tde'=3e'-Je'2tdt分部积分=3'e'-6f tde'-3t'et-6te -Je'dt]=3e/-6te+6e'+C=3e派2/-2/+2+C

倍角公式 凑微分 分部积分 换元 分部积分 分部积分

凑微分分部积分13.dx3X+ana解：原式={-号nxd)122分部积分凑微分In2xInxInx11nxdX十文-222元22x2Inx1nx+C4x22x22x2sinxcosxdx14.解：原式=sinxcos?xcosxdx凑微分=[sinx(-sinxsin x1ax+csinsin68

凑微分 分部积分 凑微分 分部积分 凑微分

xer15.d1凑微分+1微分形式不变2性+l解：原式=裂项+1分部积分X-L一一+1#+1x+me'-nle"+1)+e+1xe"-n(e+1)+Ce+1

微分形式不变 性 凑微分 分部积分 裂项

102arccosx微分dxVi-x[102accosxd(2arccosx)解：原式=11福102arcosx102arccosx+C+C2n102ln10