《高等数学》课程教学资源（课件讲稿）第四章_4.2.1（2/2）

第二节换元积分法1第一类换元法一、又叫凑微分法二、第二类换元法（代换法）三、小结思考题高等数学（上册）

一、第一类换元法（又叫凑微分法） 二、第二类换元法（代换法） 三、小结 思考题 第二节 换元积分法1

dxa+x练习：求x2+2x-32a解2直接带公式法：先化成公式形式再代dx1dxdxx2+2x-322 -(x+1)(x +1)?-4d(x + 1)-(x+1)（x+++2-(x+1)高等数学（上册）

练习：求 2  2  3  . dx x x 解2直接带公式法：先化成公式形式再代. 2  2  3  dx x x 2 1 1 4     d ( ) x x 2 2 1 1 d ln 2 a x x C a x a a x       2 2 1 2 1      d ( ) x x 1 2 ( 1) 1 3 ln ln . 4 2 ( 1) 4 1 x x C C x x             2 2 1 2 1 1       d( ( ) x ) x

1例9 求dx.xarcsinY21(G)解dxxarcsin()2arcsin1I+C= In /arcsind(arcsin-x22arcsin2练习4-2高等数学（上册）

例9 求 解 2 1 d . 4 arcsin 2 x x  x  2 1 d 4 arcsin 2 x x  x  2 1 d 2 1 arcsin 2 2 x x x                      1 d(arcsin ) 2 arcsin 2 x x   ln | arcsin | . 2 x  C 练习4-2

xdx.例10求De2解x+2xx-联合凑微分xdxeXx+x+Cd(x -eX练习：4-2自练高等数学（上册）

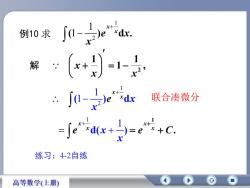
例10 求 1 2 1 (1 ) d . x x e x x    解 , 1 1 1 2 x x x            2 1 1 1     ( ) d x x e x x 1  1    d( ) x x e x x . 1 e C x x    联合凑微分 练习：4-2自练

1先化简，分母dx.例11 求2x+3+/2x-1有理化V2x+3-V2x-1原式=dx/2x+3+2x-1)(/2x+3-2x-12x+3dx』/2x-1dx[ /2x+ 3d(2x+ 3)-/2x - 1d(2x - 1)8XV(2x -1)° + C.(2x+3)3-12高等数学（上册）

例11 求 1 2 3 2 1 dx. x   x   原式    2 3 2 1 2 3 2 1 2 3 2 1 d x x x x x x x            1 1 2 3 2 1 4 4  x  dx  x  dx   1 1 2 3 2 3 2 1 2 1 8 8  x  d( x  ) x  d( x  )   1 3 1 3 (2 3) (2 1) . 12 12  x   x   C 先化简，分母 有理化

练习：求xcos x°dx;dxXdx;dx;+e+Inxdx:dx.x凑微分f[p(x)]p'(x)dx =/ f[p(x)]dp(x)高等数学（上册）

练习： 求 2 2 1 1 1 1 1 1 d ; cos d ; d ; d ; ln ; . x x x x x x e x x x x x e x x e e e x dx dx e x             f[(x)](x)dx  f[(x)]d(x) 凑微分

ev*dx =2[ev*d/x = 2eVx +C;dx? ==sinx? +C;dxx cos xC22一=In|1+e*|+C;2dx;+112dx = atctane* +C:1+ lnx((I+ Inx)=dx = [(1+ Inx)d(Inx+ 1)dx +C=x(1 + Inx)?C高等数学（上册）

2 2 2 2 2 2 2 2 2 1 1 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1                                             d C; cos cos sin C; d ln | | C; d ; tan C; ln C ( lnx) ( lnx)d(lnx ) ( l d C d ) d d n . x x x x x x x x x x x x x x x x e e x e x x dx x e e e e x e e e dx atc e e e x x x x e x e x e dx d x x x dx x x

见教材142页4、5Itan xdx和Icotxdx.例1求解tan xdx = -In cos x+ Csin xI tan xdx =dxcotxdx =sin x+ CIncosx1d(cos x) = -In cos x+ C.cosxcosxI cot xdx =dxsin x-d(sin x) = In sin x+ C.sin x（5）一般地[ f(cos x)sin xdx=-J f(cosx)d cosx sin xdx=-d cos x[f(sinx)cosxdx=Jf(sinx)dsinxcosxdx=dsinxC高等数学（上册）

例1 求 ta n x d x c o t x d x .  和  sin ta n d d co s 1 d (co s ) ln co s . co s x x x x x x x C x          解 c o s c o t d d sin 1 d (sin ) ln sin . sin x x x x x x x C x        ta n d ln c o s c o t d ln sin x x x C x x x C        （5）一般地, 见教材142页4、5

书例4.25.见教材142页公+(例2 求csc xdx式6,71sin x解csc xdxdxdxsin xsun+ cos x-+Cd(cos x) cos xxcos分母平方差，分子常数，可拆项u=cosx拆项11duu可互化21+uuMN1NM-cosxU+ C.+C22l+u1+ cosxdx = ( csc xdx = In Icsc x - cot x I +Csin x余割积分为余割减余切的绝对值的对数加C高等数学（上册）

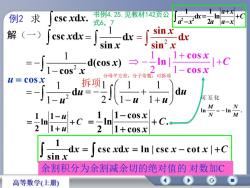
解（一） 1 d sin x x   csc xdx  2 sin d sin x x x   2 1 1 d(cos ) cos x x     u  cos x 2 1 1 du u     1 1 1 2 1 1 du u u             C u u     1 1 ln 2 1 . 1 cos 1 cos ln 2 1 C x x     拆项 例2 求 csc xdx.  1 d csc d ln | csc cot | sin x x x x x C x       余割积分为余割减余切的绝对值的 对数加C 书例4.25.见教材142页公 式6，7 分母平方差，分子常数，可拆项 2 2 1 1 d ln 2 a x x C a x a a x       1 1 2 1      cos ln | | cos x C x ln   ln . 可互化 M N N M

见教材142页公式6，7dx = ( csc xdx = In Icsc x - cot x I +Csinx余割积分为余割减余切的绝对值的对数加C类似地可推出-dx ={ sec xdx = In sec x + tan x+ Ccosx正割积分为正割加正切绝对值的对数加C高等数学（上册）

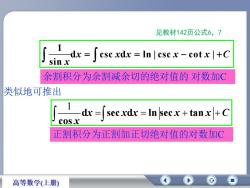
1       d sec d ln sec tan cos x x x x x C x 正割积分为正割加正切绝对值的对数加C 类似地可推出 1 d csc d ln | csc cot | sin x x x x x C x       余割积分为余割减余切的绝对值的 对数加C 见教材142页公式6，7