《高等数学》课程教学资源（课件讲稿）第五章课件_第五章第四节反常积分

第五章第四节反常积分无穷区间上的反常积分一二、天无界函数的反常积分HIGH EDUCATION PRESS机动目录上页下页返回结束

二、无界函数的反常积分 第四节 一、无穷区间上的反常积分 机动 目录 上页 下页 返回 结束 反常积分 第五章

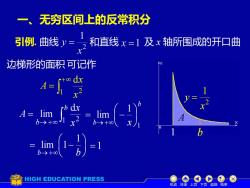
无穷区间上的反常积分一、引例.曲线和直线x=1及x轴所围成的开口曲V=边梯形的面积可记作A=WdxblimA=limJb-→+8b-→+limb→+ooHIGH EDUCATION PRESS机动目录上页下页返回结束

一、无穷区间上的反常积分 引例. 曲线 和直线 及 x 轴所围成的开口曲 边梯形的面积 2 1 x y = A 1 可记作  + = 1 2 d x x A  → + = b b x x A 1 2 d lim b b b x 1 1 lim       = − →+       = − b→+ b 1 lim 1 =1 机动 目录 上页 下页 返回 结束

定义l.设 f(x)eC[a,+),取b>a,若rblim. f(x)dxb→+oJa记作存在，则称此极限为f(x)的无穷限反常积分.b+8f(x)dx = lim(f(x)dxb-→+Ja+8这时称反常积分f(x)dx收敛；如果上述极限不存在a+8f(x)dx发散就称反常积分Ja类似地,若 f(x)EC(-o,b]，则定义brbf(x)dx = lim/f(x)dxa-aHIGH EDUCATIONPRESS机动目录上页下页返回结束

定义1. 设 f (x)C[a, + ), 取b  a, 若 存在 , 则称此极限为 f (x) 的无穷限反常积分, 记作 这时称反常积分 收敛 ; 如果上述极限不存在, 就称反常积分 发散 . 类似地 , 若 f (x)C (−, b], 则定义 机动 目录 上页 下页 返回 结束

若 f(x)EC(-80,+),则定义F-f(x)dx + limf(x)dxf(x)dx = limb→+oo Jca-8a（c为任意取定的常数）-只要有一个极限不存在，就称f(x)dx 发散HIGH EDUCATION PRESS机动目录上页下页返回结束

若 f (x)C (−, + ), 则定义 f x x c a a lim ( )d  →− f x x b b c lim ( )d  →+ + ( c 为任意取定的常数 ) 只要有一个极限不存在 , 就称 发散 . 机动 目录 上页 下页 返回 结束

若F(x)是f(x)的原函数，引入记号F(+oo)= lim F(x); F(-oo)= lim F(x)x→+8x→-8则有类似牛一莱公式的计算表达式+8= F(+o)- F(a)f(x)dx= F(x)Chf(x)dx = F(x)= F(b)- F(-00)18+8 f(x)dx = F(x)= F(+8)- F(-8)-8HIGH EDUCATION PRESS机动目录上页下页返回结束

引入记号 F( ) lim F(x) ; x→+ + = F( ) lim F(x) x→− − = 则有类似牛 – 莱公式的计算表达式 : f x x a ( )d  + = F(x) = F(+) − F(a) f x x b ( )d − = F(x) = F(b) − F(−) f (x)dx  + − = F(x) = F(+) − F(−) 机动 目录 上页 下页 返回 结束

dx+8例1.计算广义积分81+x-dx+8+8解：[arctan x+88++九Xxdx+80对吗？关(思考：81+x+8+ xdx分析：原积分发散！人+X-8HIGH EDUCATION PRESS机动目录上页下页返回结束

例1. 计算广义积分 解: + − = [arctan x ] ) 2 (  − − 2  = =  机动 目录 上页 下页 返回 结束 o x y 2 1 1 x y + = 思考: 分析: 原积分发散 !

dx+8当p>1 时收敛；p≤1例2.证明第一类p积分rp时发散证:当p =1 时有dx+8+8=[1n|x| ]=十8当p≠1时有8p1p--p因此,当p>1 时,广义积分收敛，其值为p-1当p≤1 时,广义积分发散HIGH EDUCATION PRESS机动目录上页下页返回结束

例2. 证明第一类 p 积分 证:当 p =1 时有   + = a ln x = + − +    −  = a p p x 1 1 当 p ≠ 1 时有 p 1 , p 1 1 1 − − p a p 当 p >1 时收敛 ; p≤1 时发散 . +  , 因此, 当 p >1 时, 广义积分收敛 , 其值为 ; 1 1 − − p a p 当 p≤1 时, 广义积分发散 . 机动 目录 上页 下页 返回 结束

+8ptdt(p>0)例3.计算广义积分Cpi解：原式=-=iOdt0pD+8-pte20rHIGHEDUCATION PRESS目录机动上页下页返回结束

例3. 计算广义积分 解: pt e p t − 原式 = −  + − + 0 d 1 e t p pt pt e p − = − 2 1 2 1 p = 机动 目录 上页 下页 返回 结束

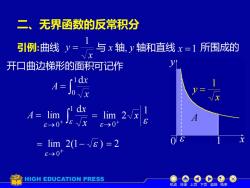
二、无界函数的反常积分引例：曲线与 x轴,y轴和直线 x=1 所围成的V=开口曲边梯形的面积可记作1dxVXdxA= limlim 2VxA8c→0+J Vx→0+ lim 2(1- Vε) = 2-0+HIGH EDUCATION PRESS机动目录上页下页返回结束

二、无界函数的反常积分 引例:曲线 与 x 轴, y 轴和直线 所围成的 开口曲边梯形的面积可记作 +  → = 1 0 d lim   x x A   1 lim 2 0 x → + = lim 2(1 ) 0   = − → + = 2 x y 1 = 0 A x y  机动 目录 上页 下页 返回 结束

定义2. 设 f(x)ε C(α,bl,而在点α 的右邻域内无界cb取ε>0,若极限 limf(x)dx存在，则称此极限为函&-0+Ja+8数f(x)在[α，b]上的反常积分,记作hf(x)dx = limf(x)dx→0+Ja+ecb这时称广义积分f(x)dx 收敛；如果上述极限不存在Cb就称广义积分f(x)dx 发散类似地,若 f(x)εC[a,b),而在b 的左邻域内无界cbrb-s则定义f(x)dx = limf(x)dx-0+JaHIGH EDUCATION PRESS机动目录上页下页返回结束

定义2. 设 f (x)C (a, b], 而在点 a 的右邻域内无界, 存在 , 这时称广义积分 收敛 ; 如果上述极限不存在, 就称广义积分 发散 . 类似地 , 若 f (x)C[a, b), 而在 b 的左邻域内无界, 若极限 数 f (x) 在 [a , b] 上的反常积分, 记作 则定义 机动 目录 上页 下页 返回 结束 则称此极限为函