《高等数学》课程教学资源（课件讲稿）第四章_4.2.1（1/2）

第二节换元积分法第一类换元法/.又叫微分法第二类换元法（代换法）三、小结思考题高等数学（上册）

一、第一类换元法（又叫凑微分法） 二、第二类换元法（代换法） 三、小结 思考题 第二节 换元积分法

一、第一类换元法（文叫微分法）问题cos2xdx =(?)sin2x+C利用复合函数，设置中间变量解决方法过程令t=2x=x:dt22sin2x + Csintcos2xdx =cos tdt=222高等数学（上册）

问题 cos 2xdx   ( )sin2x C, 解决方法 利用复合函数，设置中间变量. 过程 令 t  2x 1 1 1 2 2 2  x  t  dx  d( t)  dt, cos 2xdx  1 2  costdt   sint  C 2 1 sin2 . 2 1  x  C 一、第一类换元法（又叫凑微分法）

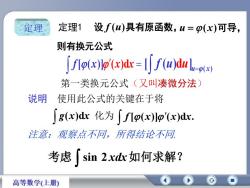
定理1定理设f(u)具有原函数，u=(x)可导，则有换元公式[f[o(x)l(x)dx= [| f (u)dulu=p(x)第一类换元公式（又叫凑微分法）说明使用此公式的关键在于将[ g(x)dx 化为 ( f[p(x)]p(x)dx.注意：观察点不同，所得结论不同考虑「sin2xdx如何求解?高等数学（上册）

设 f (u)具有原函数，    f[(x)] (x)dx   ( ) [ ( )d ] u x f u u  第一类换元公式（又叫凑微分法） 说明 使用此公式的关键在于将 g(x)dx  化为 f [(x)](x)dx.  注意：观察点不同，所得结论不同. u  ( x)可导， 则有换元公式 定理 定理1 考虑  sin 2 xdx如何求解？

解法1sin 2xdxt=2x,=x=dx = d(U211sintdtcost +Ccos2x + C:222解法2sin 2xdx2sin xcos xdx t = sin x,dt = cos xdx= 2tdt = t? +c=(sin x) +C;解法3sin2xdx t = cos x,dt = -sin xdx=2sin x cos xdxtdt = -t? +C = -(cosx) +C注：第一类换元法的中即直接令间变量可以不设出来，体现凑微分的思想高等数f(p(x)dx=f((x)d(x),P

解法1 sin 2xdx  1 1 2 2  sintdt   cost C  cos 2 ; 2 1   x  C 解法2 sin 2xdx   2 sin xcos xdx  2  2 tdt  t  c  sin  ; 2  x  C 1 1 1 2 2 2 2 t  x, x  t  dx  d( t)  dt t  sin x,dt  cos xdx 解法3 sin 2xdx   2 sin xcos xdx 2  2 tdt  t  C  cos  . 2   x  C t  cos x,dt  sin xdx          ，体现凑微分的思想 . 注：第一类换元法的中 间变量可以不设出来， 即直接令  f  x  x dx   f  x d x

令3+2x=t,解出x，代入1练习：4-2"dx = In|x|+C求dx.例1 3+2x1又解dx(3+2xdx3+2x3+2x251dl3+2x基本微分23+2x=In |3+ 2x |+C.2[ f(ax +b)dx ==[ f(ax +b)d(ax +b)（1）一般地高等数学（上册）

1 3 2 dx  x  1 ln | 3 2 | . 2   x C   f (ax b)dx   1     f (ax b)d ax b a （1）一般地 x dx x (3 2 ) 3 2 1 2 1        x dx  3  2 d x x 3 2 3 2 1 2 1     d3  2x 例1 求 1 3 2 dx.  x  又解 1dx ln x C x    基 本 凑 微 分 练习：4-2

x求例1. 1dxx+-x分子加减项法解dxdx+x11Jd(1++ x)2(1 + x)11+C1+x2(1 + x)练习：高等数学（上册）

例1.1 求 3 1 d . ( ) x x  x  解 3 1 d ( ) x x  x  3 1 1 1 d ( ) x x x      2 3 1 1 1 1 1 [ ]d( ) ( ) ( ) x x x       C x x       2 2(1 ) 1 1 1 分子加减项法 练习：

利用基本积分表的公式把被积函数中的一部分成中间变量的微分，常见的有：（类比79页公式）-1dx = =d(ax +b)dx=2dVxdx=O大axVx1"dx ==d(dx = d(In | x D;Irxn1e*dx = d(e*)a*dx :daInacos xdx = d(sin x)sinxdx =-d(cosx)sec2 xdx = d(tan x)csc2 xdx = -d(cot x)1dx = d(arcsin x)= -d(arccos x)V1-x?1dx = d(arctan x)= -d(arccot x)1+x高等数学（上册）

利用基本积分表的公式把被积函数中的一部分凑成 中间变量的微分，常见的有：（类比79页公式）     1 2 2 2 2 1 1 1 (ln | |); 1 ( ) ( ) ln cos (sin ) sin (cos ) sec (tan ) csc (cot ) 1 (arcsin ) (arccos ) 1 1 (arctan ) ( cot ) 1 n n x x x x dx d ax b a x dx d x dx d x n x e dx d e a dx d a a xdx d x xdx d x xdx d x xdx d x dx d x d x x dx d x d arc x x                    

例2求x cos x?dx解xcos x’dx =[ (cos x*)xdx凑微分11cos x dx?sin x? +C二22I(2）一般地J (x)xdx =-J f(x)dx?dx2xdx1福2练习：4-2，2Jf(x")x"dx--jf(x")dx(8)推广高等数学（上册）

例2 求 2 x cos x dx  解 2 x cos x dx  2 = (cos x )xdx  2 2 cos 1 2  x dx  凑微分 1 2 sin 2  x C （2）一般地 练习：4-2，2 （8） 推广

1推广?Jf(x")x"dxf(x")dx"二n特例两个如下，n=-1Jrd=-{ra]dx=xxxx7XX1n=2f(Vx)dx=2ff(Vx)dVxdx=2dVx.x高等数学（上册）

推广 特例两个如下

1求例3dx.x(1 + 2lnx)1凑微分11解dx =d(ln x)(1 +2lnx) x1+2lnx1d(1+ 2 ln x)1+2lnx2J:In|1+ 2Inx I+C.2f(lnx)dx = J f(ln x)d In x（3）一般地dx=dlnxxx6高等数学（上册）

例3 求 1 1 2 d . ( ln ) x x  x  解 1 1 1 2  ( ln ) d x x x 1 1 2    ln d(ln ) 凑微分 x x 1 1 1 2 2 1 2 d( ln ) ln x x     1 ln |1 2ln | . 2   x C （3）一般地