《高等数学》课程教学资源（课件讲稿）第三章课件_第三章第三节

第三章第三节泰勒公式泰勒中值定理一、天二、麦克劳林公式三、泰勒公式的应用HIGH EDUCATION PRESS机动目录上页返回下页结束

二、麦克劳林公式 第三节 一、泰勒中值定理 机动 目录 上页 下页 返回 结束 三、泰勒公式的应用 泰勒公式 第三章

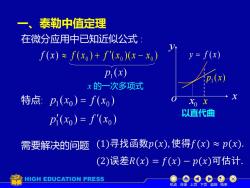
泰勒中值定理一、在微分应用中已知近似公式：y= f(x)f(x) = f(xo)+ f'(xo)(x- xopi(x)(pi(x)x的一次多项式X特点：pi(xo) = f(xo)Xo x以直代曲pi(xo) = f'(xo)(1)寻找函数p(x),使得f(x) ~ p(x)需要解决的问题(2)误差R(x) =f(x)一p(x)可估计HIGH EDUCATION PRESS机动目录上页下页返回结束

特点: ( ) 0 = f x ( ) 0 = f  x 一、泰勒中值定理 f ( x) x y y = f ( x ) o ( ) ( ) ( ) 0 0 0  f x + f  x x − x 以直代曲 0 x ( ) 1 p x 在微分应用中已知近似公式 : 需要解决的问题 x x 的一次多项式 机动 目录 上页 下页 返回 结束

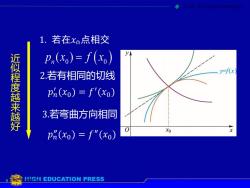
1.若在xo点相交Vp,(xo)= f (xo)近似程度越来越好y-f(x2.若有相同的切线pn(xo) = f'(xo)3.若弯曲方向相同0xoxpn(xo) = f"(xo)HH EDUCATIONPRESS

第三节 泰勒公式 第三章 微分中值定理与导数的应用 近 似 程 度 越 来 越 好 2.若有相同的切线 3.若弯曲方向相同

1.求n次近似多项式Pn(x),要求：)= f(n)(xo)Pn(xo) = f(xo), pn(xo) = f'(xo), .**, phn)(xo)Pn(x)= ao+ai(x- xo)+a2(x - xo)? + ..+ an(x - xo)n令ai+2a2(x- xo)+..+ nan(x-xo)n-1则p(x) =2 a2 +..+ n(n - )an(x - xo)n-2pn(x) =.....(n) (x)=n!anpn"中aj = pn(xo)= f(xo)ao = pn(xo)= f(xo)a2 =2P"(xo)="(xo), , an=pnn)(xo)= (n)(xo故 Pn(x)= f(xo)+ f(xo)(x-xo)+f"(xo)(x-xo)-..+ f(n)(xo)(x-xo)HIGH EDUCATION PRESS机动目录上页下页返回结束

1. 求 n 次近似多项式 要求: ( ) 2! 0 1 2 a p x n =  ( ), 0 = f  x  , ( ) 0 ( ) ! 1 a p x n n = n n ( ) 0 ( ) f x n = 故 pn (x) = ( ) 0 f x ( )( ) 0 0 + f  x x − x +  2! 1 ! 1 n n n f (x )(x x ) 0 0 ( ) + − ! 1 n 2 0 0 + f (x )(x − x ) 2! 1 机动 目录 上页 下页 返回 结束 令 pn (x) = 则 pn  (x) = pn (x) =     n p (n) (x) = n!a n ( ) 0 0 a p x = n ( ), 0 = f x ( ) 1 0 a p x n =  ( ), 0 = f  x a1 2 ( ) 2 0 + a x − x 1 0 ( ) − + + − n n  n a x x 2 2 !a 2 0 ( 1) ( ) − + + − − n n  n n a x x a0 n n a (x x ) a (x x ) a (x x ) 0 2 + 1 − 0 + 2 − 0 + + −

2.余项估计令R,(x)= f(x)- P,(x)(称为余项),则有R,(xo)= R′(xo) =... = R(n)(xo) = 0R,(x)(x-xo)n+1R',(EI)Rn(x)- R,(xo)(Si在xo与x之间)(x -xo)n+l- 0(n +1)(Si - xo)"R"(52)R,(E) - R'(xo)(三2 在 Xo 与与i 之间)(n+ 1)n(52 - xo)n-I(n+1)(-xo)"- 0R(n)(En) - R(n)(xo)R(n+1)(E)(在xo与x之间)(n +l)!(n+1)... 2(En - xo)- 0HIGH EDUCATION PRESS机动目录上页下页返回结束

) 0 ( 在 x 与 n 之 间 ( ) ( ) 1 0 + − = n n x x R x ( 1) 2( ) ( ) 0 ( ) n x R n n n n + − =    2. 余项估计 R (x) f (x) p (x) 令 n = − n (称为余项) , ( ) 0 R x n ( ) 0 R x n =  ( ) 0 0 ( ) = = R x = n  n 1 0 ( ) ( ) + − n n x x R x n n n x R ( 1)( ) ( ) 1 0 1 + −  =   ( 1)( ) ( ) 1 0 1 n n n x R + −  =   1 2 0 2 ( 1) ( ) ( ) − + −  = n n n n x R   =  ( 1)! ( ) ( 1) + = + n R n n  则有 ( ) 0 R x − n − 0 ( ) 0 R x n −  − 0 ( ) 0 ( ) R x n − n − 0 x ) 1 0 ( 在 x 与x 之 间) 1 2 0 ( 之间 在 与   x 机动 目录 上页 下页 返回 结束

Rn(x)= f(x)-pn(x)R(n+1)(E)R,(x)(在xo与x之间)n+l(n+1)!(x -xo)(n+)(x)= 0, :. R(n+1)(x)= f(n+1)(x)(nt())n+1R,(x)=(x- xo)(=在xo与x之间)(n+l)!1 f(n+)(x)|≤ M 时当在 xo的某邻域内M[n+1[R(x)|≤x- Xo(n + 1)!R,(x) = o((x - xo)")(x →xoHIGH EDUCATION PRESS机动目录上页下页返回结束

R (x) f (x) p (x) n = − n ) 0 ( 在 x 与x 之 间 ( ) 0, ( 1) = + p x n  n 1 0 ( 1) ( ) ( 1)! ( ) ( ) + + − + = n n n x x n f R x  ( ) ( ) ( 1) ( 1) R x f x n n n + +  = 当 在 x0 的某邻域内 f (n+1) (x)  M 时 ) 0 ( 在 x 与x 之 间 1 0 ( 1)! ( ) + − +  n n x x n M R x ( ) ( ( ) ) ( ) 0 0 R x o x x x x n  n = − → 机动 目录 上页 下页 返回 结束

泰勒中值定理：若f(x)在包含 xo的某开区间(a,b)内具有直到n +1阶的导数,则当 x E(αa,b)时,有f"(xof(x)= f(xo) + f'(xo)(x - xo)X1-2!(x -xo)"+ R,(x)n!c(n+1)())n+1其中 R,(x)=(x- xo)(在 xo 与x之间)(n + 1)!公式①称为f(x)的n阶泰勒公式公式②称为n阶泰勒公式的拉格朗日余项HIGH EDUCATION PRESS泰勒目录上页下页返回结束

公式 ① 称为 的 n 阶泰勒公式 . 公式 ② 称为n 阶泰勒公式的拉格朗日余项 . 泰勒中值定理 : 阶的导数 , 时, 有 ( ) 0 f x ( )( ) 0 0 + f  x x − x 2 0 0 ( ) 2 ! ( ) x x f x −  + +  n n x x n f x ( ) ! ( ) 0 0 ( ) + − R (x) + n ① 其中 1 0 ( 1) ( ) ( 1)! ( ) ( ) + + − + = n n n x x n f R x  ② 则当 ) 0 ( 在 x 与x 之 间 泰勒 目录 上页 下页 返回 结束

f"(xof(x)= f(xo)+ f'(xo)(x - xo)H+·(x-xo2!n+()Xo)n+1x(x - xo)C-Xon!(n+1)!(在xo与x之间)特例：拉格朗日中值定理(1)当 n =0 时, 泰勒公式变为f(x)=f(xo) + f'(=)(x - xo)(在xo与x之间)(2)当 n=1 时,泰勒公式变为f(x) = f(xo)+ f(xo)(x - xo)+2E在xo与x之间)可见f(x) = f(xo)+ f'(xo)(x- xo)f"()误差R(x)=(在xo与x之间)(x-Xo)2!HIGH EDUCATION PRESS机动目录上页下页返回结束

特例: (1) 当 n = 0 时, 泰勒公式变为 f (x) = ( ) 0 f x ( )( ) 0 + f   x − x (2) 当 n = 1 时, 泰勒公式变为 拉格朗日中值定理 f (x) = ( ) 0 f x ( )( ) 0 0 + f  x x − x 2 0 ( ) 2 ! ( ) x x f −  +  可见 误差f (x) = ( ) 0 f x ( )( ) 0 0 + f  x x − x +  1 0 ( 1) ( ) ( 1)! ( ) + + − + + n n x x n f  2 0 0 ( ) 2 ! ( ) x x f x −  + n n x x n f x ( ) ! ( ) 0 0 ( ) + − ) 0 ( 在 x 与x 之 间) 0 ( 在 x 与x 之 间) 0 ( 在 x 与x 之 间 ) 0 ( 在 x 与x 之 间 机动 目录 上页 下页 返回 结束

XOf(x) = f(xo) + f'(xo)(x -xo) +X-(n+)()Xo(x -x0)n+120x-xn!(n+1)!(在xo与x之间)注意到R,(x) = o[(x - xo)"]在不需要余项的精确表达式时，泰勒公式可写为Cxof(x)= f(xo) + f(xo)(x -xo)2!xo(x - Xo)" +o[(x - xo)"]公式③称为n阶泰勒公式的佩亚诺(Peano）余项HIGHEDUCATIONPRESS机动目录上页下页返回结束

公式 ③ 称为n 阶泰勒公式的佩亚诺(Peano) 余项 . 在不需要余项的精确表达式时 , 泰勒公式可写为 f (x0 ) + f (x0 )(x − x0 ) 0 ( 0 ) 2 +  2 ! ( ) x x f x −  + n n x x n f x ( ) ! ( ) 0 0 ( ) + − [( ) ] 0 n + o x − x ( ) [( ) ] 0 n n 注意到 R x = o x − x ③ 机动 目录 上页 下页 返回 结束 ( ) 0 f x ( )( ) 0 0 + f  x x − x 2 0 0 ( ) 2 ! ( ) x x f x −  + +  n n x x n f x ( ) ! ( ) 0 0 ( ) + − ) 0 ( 在 x 与x 之 间 1 0 ( 1) ( ) ( 1)! ( ) + + − + + n n x x n f 

在泰勒公式中若取 xo=0,==0x (0<0<1)f"(O)(0f(x) = f(O)+ f'(0)x2!nf(n+l)(0x)n+1x(n+1)!公式称为麦克劳林（Maclaurin由此得近似公式f(x)= f(0) + f(O)x +2!n!若在公式成立的区间上|(n+I)(x)≤M,则有误差估计式MIn+R,(x)|Vn+HIGH EDUCATION PRESS麦克劳林目录上页下页返回结束

称为麦克劳林（ Maclaurin ）公式 . 0 , (0 1) , x0 =  =  x    f (0) + f (0)x 2 +  2 ! (0) x f  + n n x n f ! (0) ( ) + 在泰勒公式中若取 f (x) = ( ) 0 f x ( )( ) 0 0 + f  x x − x +  1 0 ( 1) ( ) ( 1)! ( ) + + − + + n n x x n f  2 0 0 ( ) 2 ! ( ) x x f x −  + n n x x n f x ( ) ! ( ) 0 0 ( ) + − ) 0 ( 在 x 与x 之 间 f (x)  f (0) + f (0)x +  ( ) , ( 1) f x M n  + 则有误差估计式 1 ( 1)! ( ) + +  n n x n M R x 2 2 ! (0) x f  + n n x n f ! (0) ( ) + 若在公式成立的区间上 麦克劳林 目录 上页 下页 返回 结束 由此得近似公式