《高等数学》课程教学资源（课件讲稿）第二章_2.2.1-2.2.3

第二节求导法则与基本初等函数求导公式一、和、差、积、百商的求导法则，反函数的求导法则二、三、复合函数的求导法则四、基本求导法则与求导公式五、小结思考题经济数学微积分

一、和、差、积、商的求导法则 二、反函数的求导法则 三、复合函数的求导法则 第二节 求导法则与基本 初等函数求导公式 四、基本求导法则与求导公式 五、小结 思考题

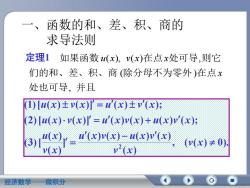
函数的和、差、积、商的求导法则定理1如果函数u(x)，v(x)在点x处可导,则它们的和、差、积、商（除分母不为零外)在点x处也可导，并且1uxtx-u(xtvx2 /u(x) v(x - u (xv(x) + u(xv (x);u(x),-"(0)() -u(x)v(x)31x#0v(x)V微积分经济数学

一、函数的和、差、积、商的 求导法则 定理1 处也可导 并且 们的和、差、积、商 除分母不为零外 在点 如果函数 在点 处可导 则它 , ( ) ( ), ( ) , x u x v x x , ( ( ) 0). ( ) ( ) ( ) ( ) ( ) ] ( ) ( ) (3)[ (2)[ ( ) ( )] ( ) ( ) ( ) ( ); (1)[ ( ) ( )] ( ) ( ); 2                   v x v x u x v x u x v x v x u x u x v x u x v x u x v x u x v x u x v x

推论n[E f(x)" = Ef(x);(1)i=1i=1[Cf(x)}= Cf'(x),C为常数;(2)业n(3) [f(x)}=f (x)f(x).. f,(x)+f(x)f (x).. f(xi=1+..+f(x)f(x).. fr(x)nV-Zf(x)f(x);?i-l k-lkti微积分经济数学

推论 (1) [ ( )] ( ); 1 1        n i i n i i f x f x (2) [Cf (x)]  Cf (x),C为常数; 1 2 1 2 1 1 2 1 1 (3) [ ( )] ( ) ( ) ( ) ( ) ( ) ( ) + ( ) ( ) ( ) ( ) ( ); n i n n i n n n i k i k k i f x f x f x f x f x f x f x f x f x f x f x f x                   

下面看一些例子例1 求= x3-2x2+sinx的导数.解 J'=3x2-4x +cosx.例2 求y= sin2x·Inx的导数.解: y = 2sin x.cosx In xy' = 2cos x .cosx . In x+ 2sin x (-sin x).ln x1+ 2sin x · cos xx= 2cos2x ln x + =sin 2x.x微积分经济数学

例1 2 sin . 求 y  x 3  x 2  x 的导数 解 2 y  3x  4x 例2 求 y  sin 2x  ln x 的导数 . 解  y  2sin x  cos x  ln x y  2cos x  cos x  ln x 2sin x ( sin x) ln x x x x 1  2sin  cos   cos x. sin 2 . 1 2cos 2 ln x x  x x  下面看一些例子

例3 求 y=tanx的导数。解 y'=(tanx)'=(xcosx(sin x)' cos x - sin x(cos x)"cos xcos? x + sin' x12sec"x2cos"xcos"x即 (tan x)' = sec’ x.cot x)'= -csc x.同理可得经济数学微积分

例3 求 y  tan x 的导数 . 解 ) cos sin   (tan )  (  x x y x x x x x x 2 cos (sin ) cos  sin (cos )  x x x 2 2 2 cos cos  sin  x x 2 2 sec cos 1   (tan ) sec . 2 即 x   x (cot ) csc . 2 同理可得 x    x

例4 求 y= secx的导数。解 j'=(secx)'=(cos x-(cosx)sin x= sec x tan x.acos? xcos'x同理可得=-cscxcotxcscx)"经济数学微积分

例4 求 y  sec x 的导数 . 解 ) cos 1   (sec )  (  x y x x x 2 cos  (cos )   sec x tan x. x x 2 cos sin  同理可得 (csc x)   csc x cot x

二、反函数的求导法则如果函数x=(y)在某区间I,内单调、可导定理2且β(y)O，那末它的反函数 y= f(x)在对应区间I内也可导，且有1dy或f'(x)dxdxp'(y)dy即反函数的导数等于直接函数导数的倒数经济数学微积分

二、反函数的求导法则 定理2 . ( ) 1 ( ) , ( ) 0 , ( ) ( ) y f x I y y f x x y I x y           内也可导 且有 且 那末它的反函数 在对应区间 如果函数 在某区间 内单调、可导 即 反函数的导数等于直接函数导数的倒数. d 1 d d x d y y x 或 

证任取xIx，给x以增量△x（Ax0,x+△xI）Ay # 0,由y= f(x)的单调性可知1Ay于是有：f(x)连续,ArArAy又知β'(y)± 0:: Ay →0 (△x →0),11Aylim:: f'(x) = limAxp'(y)Ax=0 AxAy-→0Ay1即 f'(x)p'(y)微积分经济数学

证 , x 任取x  I 给x以增量x 由y  f (x)的单调性可知 y  0, 于是有 , 1 y x x y       f (x)连续, y  0 (x  0), 又知( y)  0 x y f x x       0 ( ) lim y y x      1 lim 0 ( ) 1  y  . ( ) 1 ( ) y f x  即   ( 0, ) x x  x  x  I

例7 求函数 y=arcsin x的导数.解：y=arcsinx=x=siny1111dy1dxdx(sin y)cosy -sin? y-xdy元或解内单调、可导，：x=siny在I,2'且 (sin y)'= cos y> 0, 在IxE(-1,1)内有1111(arcsin x)':(sin y)'I - sin’cos y(arccosx)'同理可得(arctanx)arccotx)微积分经济数学

. 1 1 ( cot ) 2 x x  arc    例7 求函数 y  arcsin x的导数. 或解 ) , 2 , 2 sin 在 ( 内单调、可导    x  y I y   且 (sin y)  cos y  0, 在I x (1,1)内有 (sin ) 1   y cos y 1  y 2 1 sin 1   . 1 1 2  x  . 1 1 (arccos ) 2 x x  同理可得    ; 1 1 (arctan ) 2 x x    (arcsin x) 2 2 d 1 1 1 1 1 = . d dx (sin ) cos 1 sin 1 dy y y x y y y x           解：y=arcsinx x=siny

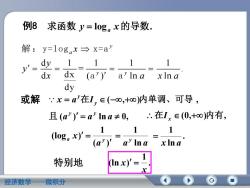
例8 求函数 y=log。x的导数.解： y=log.x→ x=a1111dy2dxdx(a")" a'lnaxlnady或解牟：x=a在I,E(-80,+oo)内单调、可导，:: 在I, E(0,+)内有,且 (a)=aIna±0,111(loga x)"(a")aInaxlna1特别地(ln x)'=xE微积分经济数学

例8 求函数 y log x的导数.  a (a )  a ln a  0, 且 y y 在 (0,)内有, x I ( ) 1 (log )    a y a x a a y ln 1  . ln 1 x a  或解  在  (,)内单调、可导 , y y  x a I 特别地 . 1 (ln ) x x   d 1 1 1 1 = . d dx ( ) ln ln dy y a y y x y y x a x a        解：y=log x=a a a