《高等数学》课程教学资源（课件讲稿）第一章_1.5.1-1.5.3

第七节函数的连续性函数的连续性的概念、二、函数的间断点三、初等函数的连续性四、小结思考题高等数学（上册）

一 、函数的连续性的概念 二、函数的间断点 四、小结 思考题 第七节 函数的连续性 三、初等函数的连续性

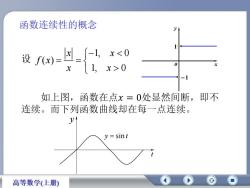
函数连续性的概念x0x-1如上图，函数在点x三0处显然间断，即不连续。而下列函数曲线却在每一点连续yy=sint高等数学（上册）

y x 1  1 o 1, 0 ( ) 1, 0 x x f x x x        设 函数连续性的概念 y  sin t t y

同学们画出下面两个函数的图像，并观察这两个函数的图像有什么本质的不同？x,x>0x,x≥0f(x) =1,x= 0g(x)-x,x<o-x,x<o请同学们从严格的理论上解释该不同，高等数学（上册）

同学们画出下面两个函数的图像，并观察 这两个函数的图像有什么本质的不同? , 0 , 0 ( ) 1, 0 ( ) , 0 , 0 x x x x f x x g x x x x x                  请同学们从严格的理论上解释该不同

函数的连续性(continuity)一1.函数的增量(increment)设变量u从它的初值u,变到终值u,则Au=u,-ui称为变量 u的增量注意：(1)△u可正可负;(2)△u 是一个整体，不能看作 △与u的乘积。高等数学（上册）

一、函数的连续性(continuity) 1.函数的增量(increment) . 2 1 1 2 称为变量 的增量 设变量 从它的初值 变到终值 则 u u u u u u u    注意：(1) u 可正可负； . (2) 与 的乘积 是一个整体，不能看作 u u 

设函数 f(x)在U(x,)内有定义 当x在U(x,)内由x变到x+△x时,称Ax为自变量 x在点x的增量；相应地，函数y从f(x)变到f(x+△x)Ay = f(xo + Ax) - f(xo)称为函数 f(x)相应于△x的增量，yyy= f(x)y= f(x)AyAyArAxo10lXo + Ar xXo + Arxxoxo高等数学（上册）

的增量；相应地，函数 从 变到 ， 内由 变到 时，称 为自变量 在点 设函数 在 内有定义 当 在 ( ) ( ) ( ) ( , ) , ( , ) 0 0 0 0 0 0 0 y f x f x x x x x x x x f x U x x U x        ( ) . ( ) ( ) 0 0 称为函数 f x 相应于 x的增量 y f x x f x       x y 0 x y 0 0 x x  x 0 y  f ( x) x 0 x x  x 0 x y y y  f ( x)

2.函数连续的定义1、2:←limAy=0函数f(x)在,点处连续 lim[f(x)- f(x)]=O, x=x +△xAr-0X-→Xo8-8定义lim f(x)= f(%V>0,3>0,使当0<x-x时X-Xo恒有|f(x)-f(x)/<右连续←f(% -0)=f(% +0)=f(%左连续若函数fx）在点x处连续，则称x为函数的连续点。连续点x：limf(x)=f(xo)若函数fx）在点处不连续，则称x为函数的间断点。间断点xa：limf(x）≠f(xo）x→xo高等数学（上册）

2.函数连续的定义1、2： 0 lim 0 x y      0 0 0 lim[ ( ) ( )] 0 . x x f x f x x x x     ，   0 0 lim ( ) ( ) x x f x f x    fx00 fx00 fx0 0 函数f(x)在x点处连续 0 0 0, , , ( ) ( ) . 0 0 x x f x f x               定义 使当 时 恒有

从这个定义我们可以看出，函数f(x)在点 x处连续，必须满足以下三个条件：(1)函数f(x)在点x.处有定义;(2）极限 limf(x)存在，即x→Xolim f(x)= lim f(x)x-Xox-xo(3) lim f(x)= f(x,) :即：[函数在某点连续等价于函数在该点的极限存在且等于该点的函数值高等数学（上册）

从这个定义我们可以看出，函数 f (x)在点 x0 处连续，必须满足以下三个条件： （1）函数 f (x)在点 0 x 处有定义； （2）极限 lim ( ) 0 f x xx 存在，即 lim ( ) lim ( ) 0 0 f x f x x x x x      （3）lim ( ) ( )0 0 f x f x x x   . 即：函数在某点连续等价于函数在该点的极 限存在且等于该点的函数值

x±0,xsin例1 试证函数f(x)=在x= 0x0,x = 0,处连续证 limxsin==0,x→0x又 f(0)= 0,lim f(x) = f(O),x->0由连续定义知函数 f(x)在x=0处连续高等数学（上册）

例1 . 0 0, 0, , 0, 1 sin ( ) 处连续 试证函数 在         x x x x x f x 证 0, 1 lim sin 0   x x x  又 f (0)  0, 由连续定义知 函数 f ( x)在 x  0处连续. lim ( ) (0), 0 f x f x  

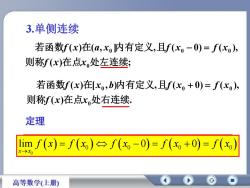
3.单侧连续若函数f(x)在(a,xj内有定义,且f(x-0)= f(x)则称f(x)在点x.处左连续若函数f(x)在[xo,b)内有定义,且f(x。+0)= f(x)则称f(x)在点x.处右连续定理lim f(x)= f(x) f(x -0)= f(xo +0) = f(x)L>XO高等数学（上册）

3.单侧连续 ( ) ; ( ) ( , ] , ( 0) ( ), 0 0 0 0 则称 在点 处左连续 若函数 在 内有定义 且 f x x f x a x f x   f x 定理 ( ) . ( ) [ , ) , ( 0) ( ), 0 0 0 0 则称 在点 处右连续 若函数 在 内有定义 且 f x x f x x b f x   f x           0 0 0 0 0 0 lim 0 f x f x f x f x f x x x                  0 0 0 0 0 lim 0 0 x x f x f x f x f x f x       

x + 2,，x≥0例2 讨论函数 f(x)=在x=0处的x-2, x<0,连续性。解 lim f(x)= lim(x+2) = 2= f(0),X-0x-→0+lim f(x) = lim(x -2)= -2± f(0)x-→0x→0右连续但不左连续，故函数f(x)在点x=0处不连续高等数学（上册）

例2 . 0 2, 0, 2, 0, ( ) 连续性 讨论函数 在  处的         x x x x x f x 解 lim ( ) lim( 2) 0 0       f x x x x  2 f (0), lim ( ) lim( 2) 0 0       f x x x x  2 f (0), 右连续但不左连续 , 故函数 f (x)在点x  0处不连续