《线性代数》课程教学资源（课件讲稿，B）第四章特征值与特征向量_4-4实对称矩阵的相似对角化

第四章S4实对称矩阵的相似对角化一、实对称矩阵的性质二、实对称矩阵对角化的方法加油！

§4 实对称矩阵的相似对角化 第四章 一、实对称矩阵的性质 二、实对称矩阵对角化的方法

实对称矩阵的性质定理1实对称矩阵的特征值都是实数定理2 实对称矩阵的不同特征值的特征向量是正交的证明：设 Pi,P,是对称矩阵A的不同的两个特征值,, 的特征向量,即 Ap= Pi, Ap2= P2,:A=AT:. apT =(aP)T =(Ap)= pTAT = pTA,于是 p = pAp = pT(p2) =p2加油！

定理1 实对称矩阵的特征值都是实数. 一、实对称矩阵的性质 定理2 实对称矩阵的不同特征值的特征向量是正交的. 1 2 1 2 , , , p p A   设 是对称矩阵 的不同的两个特征值 的特征向量 即 证明: 1 1 1 2 2 2 Ap p Ap p     , ， , T A A  1 1 1 1 1 ( ) ( ) T T T      p p Ap 1 1 , T T T   p A p A 于是 1 1 2 1 2 1 2 2 ( ) T T T   p p p Ap p p   2 1 2 , T   p p

= ( -)pTp2 = 0.，:. pTp2=0即p,与p,正交: 2 ± 22,定理3设A为n阶实对称矩阵,则有正交矩阵C使CTAC=C-AC=Λ,其中Λ是以A的n个特征值为对角元素的对角矩阵加油！

1 2 1 2 ( ) 0. T      p p , 1  2 . 1 2 0 即p1与p2正交 T   p p 1 , , , 3 . T A n C C AC C AC A n      设 为 阶实对称矩阵 则有正交矩阵 使 其中 是以 的 个特征值 为对角元素的对 定 角矩阵 理

实对称矩阵对角化的方法：1.求A的特征值2.由(a,I-A)x =0,求出A的特征向量3.将特征向量正交化：4.将特征向量单位化：5.以特征向量为列向量写出正交矩阵加油！

3.将特征向量正交化; 4.将特征向量单位化； 2. ( ) 0, ; i 由  I A x A   求出 的特征向量 5.以特征向量为列向量写出正交矩阵. 1.求A的特征值 实对称矩阵对角化的方法:

004例 设A=I，求正交矩阵C，使C-1AC031031为对角形矩阵解(1)第一步 求A的特征值002-40-312I-A== (a - 2)( - 4)012-3得特征值2, =2, 2 = 2 = 4加油！

2    ( 2)( 4) ,   2, 4. 得特征值 1  2  3  1 4 0 0 0 3 1 0 1 3 . A C C AC             设 ，求正交矩阵 ，使 为对角形矩阵 解 (1)第一步 求A的特征值 例 4 0 0 0 3 1 0 1 3 I A         

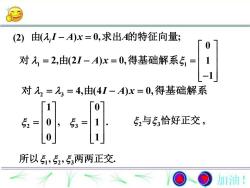
(2) 由(a,I-A)x = 0,求出A的特征向量;0对 , = 2,由(2I - A)x = 0,得基础解系, =L-1 对 , = , = 4,由(4I -A)x =0,得基础解系03,与,恰好正交，52 = 10 E3三0所以,52,5,两两正交加油！

1 1 0 2, (2 ) 0, 1 1   I A x                对 由 得基础解系 2 3 2 3 4, (4 ) 0, 1 0 0 1 , . 0 1   I A x                             对 由 得基础解系 ,  2与 3恰好正交 , , . 所以 1  2  3两两正交 ( ) 0, ; i (2) 由  I A x A   求出 的特征向量

(3)再将 51, 52,5,单位化0011152V2i=1,2,3)得0,n3 =n =n=5,01172/20(4)以n,n2,n,为列向量得正交矩阵1V2P=(n1,N2,ns)=2172加油！

1 2 3 (3) , , 再将    单位化 1 2 3 0 0 1 1 1 2 2 , , . 0 1 0 1 2 2                                                   1,2,3 i i i i    令   得 1 2 3 (4) , , 以   为列向量得正交矩阵  1 2 3  0 1 0 1 1 0 , , 2 2 1 1 0 2 2 P                      

002则C-1AC =CT AC =0040-加油！

1 200 . 0 4 0 0 0 4 T C AC C AC              则

例已知实对称矩阵A的三个特征值为2,=2,2,=2,=1213且对应与,,的特征向量是pz=1 , P =-3L-1(1)求A的对应于,=2的特征向量：(2)求矩阵A.xi解：(1)设A的对应于,=2的特征向量为p,=1X2X3加油！

1 2 3 2 3 2 3 1 2, 1 1 2 , 1 3 1 3 (1) 2 (2) . A p p A A                                   例 已知实对称矩阵 的三个特征值为 且对应与 的特征向量是 ， 求 的对应于 的特征向量； 求矩阵 1 1 1 2 3 (1) 2 x A p x x              解: 设 的对应于 的特征向量为

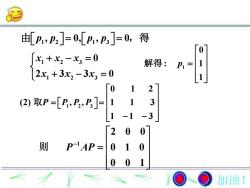
由[P1,P2]=0,[P1,P]=0,得0Xi +x, - x = 0解得：Pi=12x +3x, -3x = 01023(2) 取P=[P,P2,P, =1-31002则P-1AP =0000加油！

1 2 1 3     p p p p , 0, , 0   由    ，得 1 2 3 1 2 3 0 2 3 3 0 x x x x x x          1 0 : 1 1 p            解得 1 2 3 0 1 2 (2) , , 1 1 3 1 1 3 P P P P                   取 1 200 0 1 0 0 0 1 P AP             则