《线性代数》课程教学资源（课件讲稿，B）第一章矩阵及其初等变换_1-1矩阵及其运算2/2

第一章矩阵及其初等变换加油！

第一章 矩阵及其初等变换

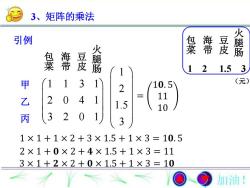
3、矩阵的乘法火腿肠引例包海豆火腿肠菜带皮包海豆F皮菜带121.53(元)3171甲(10.5)21120411.510(320丙31×1+1×2+3×1.5+1×3=10.54×15+1×3=112×1+0×2-3 × 1= 10X3加油！

3、矩阵的乘法 引例 1 1 3 1 2 0 4 1 3 2 0 1           甲乙丙 12 1.53             包菜 海带 豆皮 火腿肠 包菜 海带 豆皮 火腿肠 1 2 1.5 3 （元）

矩阵的乘法1.线性变换设变量y,J2,…ym能用变量xj,Xz,,x,线性表示yi =auX, +ai2x2 +...+ainxnJ, = a2ix, +a22X, +... +a2nXn,Jm=amiXi+am2X,+...+amnXn其中系数a,(i=1,2,,m,j=1,2,…,n)为常数，这种从变量x,xz,,x,到变量yj,J2,…ym的变换叫做线性变换加油！

1 2 1 2 1 11 1 12 2 1 2 21 1 22 2 2 1 1 2 2 1 2 1 2 , , , , , , , , ( 1, 2, , , 1, 2, , ) , , , , , m n n n n n m m m mn n ij n m y y y x x x y a x a x a x y a x a x a x y a x a x a x a i m j n x x x y y y                       设变量 能用变量 线性表示， 其中系数 为常数，这种从 变量 到变量 的变换叫做线性变换. 矩阵的乘法 1.线性变换

ail(121an2(2)a2n此线性变换的系数构成的m×n矩阵为aaamlm2mn称为线性变换的系数矩阵yi=aiix+ai2x+a13x设两个线性变换J2=a21X+a22X2+a23xX, = biuti + bi2tX, = b21ti + b22tXg = b3iti + b32t,加油！

11 12 1 21 22 2 1 2 . n n m m mn a a a a a a m n a a a              此线性变换的系数构成的 矩阵为 称为线性变换的系数矩阵 1 11 1 12 2 13 3 2 21 1 22 2 23 3 1 11 1 12 2 2 21 1 22 2 3 31 1 32 2 y a x a x a x y a x a x a x x b t b t x b t b t x b t b t                     设两个线性变换

V=axi+a1x+a13x设两个线性变换y2=a21+a22X2+a23x3Xi = buiti + bi2t2Xz = b21t + b22t2Xg=b3iti+b32t2ba12130D2b2a122a2321bbo31加油！

1 11 1 12 2 13 3 2 21 1 22 2 23 3 1 11 1 12 2 2 21 1 22 2 3 31 1 32 2 y a x a x a x y a x a x a x x b t b t x b t b t x b t b t                     设两个线性变换 11 12 13 21 22 23 a a a a a a       11 12 21 22 31 32 b b b b b b          

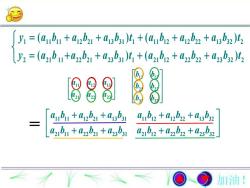
yi =(aubu + a12b21 + a13b31)t, + (au,b12 + a2b22 +a13b32)ty2 =(a21b1+a22b2 + a23b31)t +(a2bi2 + a22b22 +a23b32)t,abu+arba +aibaub12+a.b22+a.baz,b12 + a2b22 +a23b3a21bi1 +a22b21 +a23b加油！

1 11 11 12 21 13 31 1 11 12 12 22 13 32 2 2 21 11 22 21 23 31 1 21 12 22 22 23 32 2 ( ) ( ) ( ) ( ) y a b a b a b t a b a b a b t y a b a b a b t a b a b a b t                11 11 12 21 13 31 11 12 12 22 13 32 21 11 22 21 23 31 21 12 22 22 23 32 a b a b a b a b a b a b a b a b a b a b a b a b               11 12 13 21 22 23 a a a a a a       11 12 21 22 31 32 b b b b b b           =

定义4设A=(a)是一个m×p矩阵,B=(b.)是一个p×n矩阵作m×n矩阵C=(c,)，其中C, = ab, +anba, +.+agb -2aikbkjk=1矩阵C称为矩阵A与矩阵B的乘积，记作C=AB加油！

1 1 2 2 1 ( ) , ( ) , ( ) ij ij ij p ij i j i j ip pj ik kj k A a m p B b p n m n C c c a b a b a b a b C A B C AB               设 是一个 矩阵 是一个 矩阵 作 矩阵 ，其中 ， 矩阵 称为矩阵 与矩阵 的乘积，记作 定义4

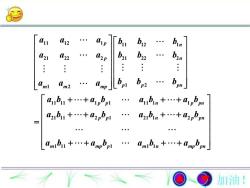
anl2baabr21Tb2b(n)(22anp2n..bbbaaapp2pnm2mlmpa,bu+a0a.bDIpn2a2tbu +..+a2pbpl+..+a..baz,bin0pnbambu +..+a....h+..+a..a..0mimpnDmppn加油！

11 12 1 11 12 1 21 22 2 21 22 2 1 2 1 2 11 11 1 1 11 1 1 21 11 2 1 21 1 2 1 11 1 1 1 p n p n m m mp p p pn p p n p pn p p n p pn m mp p m n mp pn a a a b b b a a a b b b a a a b b b a b a b a b a b a b a b a b a b a b a b a b a b                                                       

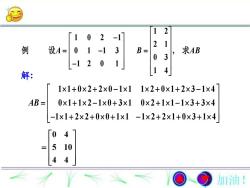
210221例设A=01-13求ABB =030241解：1×2+0×1+2×3-1×41×1+0×2+2×0-1×1AB =0×1+1×2-1×0+3×10×2+1×1-1x3+3×4-1×1+2×2+0×0+1×1 -1×2+2×1+0×3+1×4041054加油！

1 2 1 0 2 1 2 1 0 1 1 3 , 0 3 1 2 0 1 1 4 A B AB                            例 设 求 解: 1 1 0 2 2 0 1 1 1 2 0 1 2 3 1 4 0 1 1 2 1 0 3 1 0 2 1 1 1 3 3 4 1 1 2 2 0 0 1 1 1 2 2 1 0 3 1 4 AB                                                        0 4 5 10 4 4           

乘法性质：设下列矩阵都可以进行有关运算1. A(BC) = (AB)C2. k(AB)=(kA)B = A(kB)(k是数)3. A(B+C)= AB+AC(B + C)A = BA + CA加油！

乘法性质：设下列矩阵都可以进行有关运算 3. ( ) ( ) A B C AB AC B C A BA CA       2 . ( ) ( ) ( ) ( ) k A B k A B A k B k   是 数 1. ( ) ( ) A BC AB C 