《高等数学》课程教学资源（课件讲稿）第六章_6.2定积分在几何上的应用

第二节定积分在几何上的应用平面图形的面积二、旋转体的体积三、平面曲线的孤长四、小结

第二节 定积分在几何上的应用 • 一、平面图形的面积 • 二、旋转体的体积 • 三、平面曲线的弧长 • 四、小结

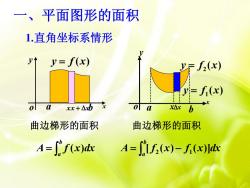
一、平面图形的面积1.直角坐标系情形yty= f(x)yE f(x)y= fi(x)XoTaxx +AxbxArolba曲边梯形的面积曲边梯形的面积A= f'f(x)dxA = I'lf,(x)- f(x)]dx

曲边梯形的面积   b a A f (x)dx 曲边梯形的面积    b a A [ f (x) f (x)]dx 2 1 x y o y  f (x) a xx  xb 1.直角坐标系情形 ( ) y  f1 x ( ) y  f2 x a b xx x y o 一、平面图形的面积

例1计算由两条抛物线y2=x和y=x2所围成的图形的面积。X=y?解两曲线的交点(0,0) (1,1)y=x?.选x为积分变量xE[0,1]面积元素 dA=(Vx-x2)dx[-]--A=f'(Vx-x")dx=

解 两曲线的交点 (0,0) (1,1) 面积元素 dA ( x x )dx 2   选 x 为积分变量 x[0,1] A ( x x )dx 2 1 0    1 0 3 3 3 2 2 3         x x . 3 1  2 y  x 2 x  y 2 2 1 . 例 计算由两条抛物线y x y x   和 所围成的 图形的面积

例2计算由曲线y=x3-6x和y=x所围成的图形的面积y=x3 -6x10解?两曲线的交点y=x2..y = x3 - 6xy=xX-2-13→(0,0), (-2,4),(3,9)2.5选x为积分变量xE[-2,3](1) xE[-2, 0], dA =(x3 -6x-x°)dx(2) x E[0,3], dA, =(x2 -x3 +6x)dx

解 两曲线的交点  (0,0), (2,4), (3,9).       2 3 6 y x y x x 选 x 为积分变量 x[2, 3] (1) x[2, 0], dA (x 6x x )dx 3 2 1    (2) x[0,3], dA (x x 6x)dx 2 3 2    2 y  x y x 6x 3   3 2 2 6 . 例 计算由曲线y x x y x    和 所围成的 图形的面积

于是所求面积 A= A, + A,A= J,(x3 -6x - x")dx+ f'(x2 - x +6x)dx25312说明：注意各积分区间上被积函数的形式问题：积分变量只能选x吗？

于是所求面积 A  A1  A2 A (x 6x x )dx 2 0 2 3     (x x 6x)dx 2 3 3 0     . 12 253  说明：注意各积分区间上被积函数的形式． 问题：积分变量只能选 x 吗？

例3计算由曲线y2=2x和y=x-4所围成的图形的面积yy? = 2xy+dy解两曲线的交点y[y? =2x0Xy=x-4y=x-4 (2,-2), (8,4)选为积分变量yE[-2,4]Ly+4-:dA = 18.dA =A=dy2-2

解 两曲线的交点  (2,2), (8,4).       4 2 2 y x y x 选 y 为积分变量 y[2, 4] dy y dA y          2 4 2 18. 4 2    A dA 2 3 2 4 . 例 计算由曲线y x y x    和 所围成的 图形的面积 x y 2x 2  o y y  x  4 y y  d y

x = p(t)如果曲边梯形的曲边为参数方程(y =y(t)曲边梯形的面积A = I" f(x)dx = I~y(t)p'(t)dt.(其中α和β对应曲线起点和终点的参数值)在[α,β]或[β,α]上x=β(t)具有连续的导数y=y(t)连续

如果曲边梯形的曲边为参数方程      ( ) ( ) y t x t   曲边梯形的面积 ( ) ( ) ( ) . b a A f x dx t t dt         (其中  和 对应曲线起点和终点的参数值) [ ] [ , ] ( ) ( ) . x t y t         在 , 或 上 具有连续的导数， 连续

L例4 求椭圆1的面积+62x=acost解椭圆的参数方程y=bsint由对称性知总面积等于4倍第一象限部分面积A = 4f" ydx =4f" bsintd(acos t)2sin tdt = πab.= 4ab

解 椭圆的参数方程      y b t x a t sin cos 由对称性知总面积等于4倍第一象限部分面积．   a A ydx 0 4   0 2 4 bsin td(acost) ab tdt    2 0 2 4 sin  ab. 2 2 2 2 4 1 . x y a b 例 求椭圆   的面积

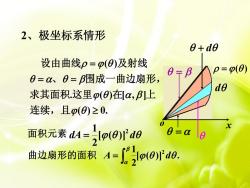
2、极坐标系情形0+de设由曲线p=β(0)及射线p= β(0)0=β=α、=β围成一曲边扇形de求其面积.这里β(0)在[α,β]上连续，且β()≥0.?X0:=α面积元素 dA=[(0)do6曲边扇形的面积 A=[,lo(0)"de

o x    d      d 面积元素 dA   d 2 [ ( )] 2 1  曲边扇形的面积 [ ( )] . 2 1 2      A d       ( ) 2、极坐标系情形 ( ) . ( ) [ , ] ( ) 0.                  设由曲线 及射线 、 围成一曲边扇形， 求其面积 这里 在 上 连续，且

例5 求由双纽线p2=a2cos20所围成的图形的面积解日由对称性知总面积=4倍第一象限部分面积4y=xAA=4A24=acos20cos2d0 = a?4A=a02

解 由对称性知总面积=4倍第 一象限部分面积 A  4A1    A a cos 2 d 2 1 4 4 0 2   . 2  a y  x  cos2 2 2  a A1 2 2 5 cos 2 . 例 求由双纽线   a 所围成的 图形的面积