《线性代数》课程教学资源（课件讲稿，B）第四章特征值与特征向量_4-3n维向量空间的正交性

第四章S3n维向量空间的正交性一、内积的定义及性质二、向量的长度及性质三、n维向量的正交性四、施密特正交化方法加油！

§3 n维向量空间的正交性 第四章 一、内积的定义及性质 二、向量的长度及性质 三、n维向量的正交性 四、施密特正交化方法

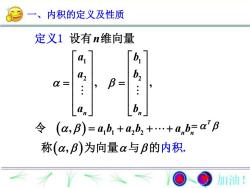
一、内积的定义及性质定义1设有n维向量Dab,a2α =b令 (α,β)=ab, +a,b, +...+a,b=α"β11称(α,β)为向量α与β的内积.加油！

    1 1 2 2 1 1 2 2 , , , , . n n n n n a b a b a b a b a b a b                                       设有 维向量 令 称 为向量 与 定 1 的内积 义 一、内积的定义及性质 T   

内积的运算性质(其中α,β,为n维向量,k为实数)：(1)(α,α)≥0,且当α 0时有(α,α)>0(2)(α,β) =(β,α);(3)(kα,β) = k(α,β);(4)(α+β,)=(α,)+(β,),加油！

内积的运算性质 其中   , , , : 为n k 维向量 为实数 (2) , , ;         (3) , , ; k k         (4) , , , .                (1) , 0, 0 , 0;          且当 时有 

二、向量的长度及性质定义2(α,α) = ya +a +...+a称为向量α的长度(或范数)，记作α向量的长度具有下述性质：1.非负性 当α±0时,α>0;当α=0时,α=0;2.齐次性 I/αl= [α;3.三角不等式α+β≤α+β加油！

定义2   2 2 2 1 2 , . n   a a a       称为向量 的长度(或范数)，记作 向量的长度具有下述性质： 1. 0 , 0; 0 , 0; 非负性 当        时 当 时 2. ; 齐次性     3. . 三角不等式        二、向量的长度及性质

若α=1,则称α为单位向量.如果α±0,由长度的概念得就是一个单位向量a1用非零数乘以向量α得到一个与α同方向的α单位向量，通常称为把向量α单位化加油！

若    1 , . 则 称 为 单 位 向 量 1   0, .  如 果  由 长 度 的 概 念 得 就 是 一 个 单 位 向 量 1 .     用非零数 乘以向量 得到一个与 同方向的 单位向量，通常称为把向量 单位化

(α,β)≤ αl 柯西-施瓦茨不等式当且仅当α与β线性相关时等号成立。(α,β)定义3当α→ 0,|β± 0时,θ = arccos Ilal// ll称为n维向量α与β的夹角，记为(α，β)加油！

 ,  0, 0 , arccos n            定义3 当    时 称为 维向量 与 的夹角，记为 ， 柯西-施瓦茨不等式：     , ,   当 且 仅 当   与 线 性 相 关 时 等 号 成 立

三、n维向量的正交性当(α,β)=0时，称向量α与β正交.定义5一组两两正交的非零向量称为正交向量组，[2]0例：α,=0,α,01定理正交向量组是线性无关向量组反之不成立，即线性无关向量组不一定正交加油！

定义5 一组两两正交的非零向量称为正交向量组． 三、n维向量的正交性 当    , 0   时，称向量 与 正交. 1 2 3 2 0 1 0 , 1 , 0 1 0 2                                      例： 定理 正交向量组是线性无关向量组. 反之不成立，即线性无关向量组不一定正交

定理正交向量组是线性无关向量组证明设有α,αz,,αm是正交向量组,k,α, +k,α, +...+kmαm=0用a,与等式两边做内积,得k,(α,α,)=0 i=1,2,..,m由α;≠0,有(α,α,)>0,从而得k, =0 i=1,2,...,m.故α,αz,,αm线性无关加油！

由   i i i   0, , 0, 有  从而得 0 1, 2, , . i k i m   1 2 , , , . 故   m 线性无关 k i m i i i  , 0 1,2, ,    定理 正交向量组是线性无关向量组. 证明 1 1 2 2 0 m m k k k        , i 用a 与等式两边做内积 得 1 2 , , , 设有   m 是正交向量组

例 已知α,=求非零向量α3,-2=11,α,1I使α,αz,α,构成正交向量组加油！

1 2 3 1 2 3 1 1 , , 1 2 1 1 , , .                              例 已知 求非零向量 使 构成正交向量组

2.标准正交向量组α,α,,.,α,满足:(1) (α,α,)=0,(i+ j,α, ±0,α, ±0)(2) α;=1, (i =1, 2,., s)则称α,αz,，α,为标准(规范)正交向量组。如 。, =(1, 0,.., 0),8, =(0, 1, .., 0), ., ·, =(0, 0, , 1)是R"的标准正交基·α, =(0,1, 0)厂是R"的标准正交基，加油！

2. 标准正交向量组       1 2 1 0 , 0 , 0, 1, , 0 , , 0, 0, , 1 n 如       ，   1 2 3 1 1 1 1 0 0 0 ,1, 0 2 2 2 2                    ， ， ， ，             1 2 1 2 , , , 1 , 0 , , 0, 0 2 1, 1, 2, , . s i j i j i s i j i s                  满足： 则称 ， ， ， 为标准 规范 正交向量组 R . 是 n 的标准正交基 R . 是 n 的标准正交基