《高等数学》课程教学资源（课件讲稿）第一章_1.4.3-1.4.4

第六节无穷小的比较高等数学（上册）

第六节 无穷小的比较

、无穷小的比较例如,0lim x = 0; limx? =: lim sin x =x->0x->0x-0所以，当x→时,x,x2,sinx都是无穷小limx?比3x趋于0要快得多；高阶的无穷小= 0,观察各极限x=0 3x0-0型)sin xsinx与x大致相同;等价的无穷小limx-→0xsin xsin xlim=oo.sinx比x2要慢低阶的无穷小limx-0x-→0xx极限不同，反映了趋于零的“快慢”禾程度不同高等数学（上册）

一、无穷小的比较 例如, x x x 3 lim 2 0 x x x sin lim 0 2 0 sin lim x x x 2 所以,当x  0时, x , x ,sin x 都是无穷小. 极限不同, 反映了趋于零的“快慢”程度不同. 2 x 比3x趋于0要快得多; sin x与x大致相同 ;  0, 1, 0 sin 1 lim( ) . x x  x x     观 察 各 极 限 0 (0 型) sin . x比 x 2 要慢 2 0 0 0 lim ;lim ;limsin . x x x x x x      

定义：设α.β是同一过程中的两个无穷小，且α±0() 如果 lim B=0 就说β是比α高阶的无穷小αo(α)记作β=o(α);因此代入得lim=0(2)如果 lim B=80，就说β是比α低阶的无穷小αβ(3)如果 limP=C±0,就说β与α是同阶的无穷小αβ特殊地,如果lim=1,则称β与α是等价的无穷小α记作α～ βB(4)如果 lim:C≠0.k>0.就说β是α的k阶的Qt无穷小高等数学（上册）

(1) l ) im 0 ( , o         如果 ，就说 是比 高阶的无 记 穷小 作 ； 定义:设,是同一过程中的两个无穷小,且  0. (3) lim C 0, ;     如果   就说 与 是同阶的无穷小 lim , ; 1 ; ~       特殊地，如果  则称 与 是等价的无穷小 记作 ( ) lim     ２ 如果  ，就说 是比 低阶的无穷小． (4) lim 0, 0, . k C k k     如果    就说 是 阶的 无穷小 的 ( ) lim 0 o   因此代入得 

例如,0.(1):lim即 x2 = 0(3x) (x → 0)x0 3x：当x→0时，x2是比3x高阶的无穷小；0(3x)因此lim03xsinx1(2):lim即sinx~x (x→0)x→0x当x→0时，sinx与x是等价无穷小。定理1β与α是等价无穷小的的充分必要条件为β=α+o(α).称α是β 的主要部分，房高等数学（上册）

2 0 lim x 3 x  x   0 sin lim x x  x   0 3 ;  当 x  时，x 2 是比 x 高阶的无穷小 (3 ) ( 0). 即 x 2  o x x   当 x  0 时，sin x 与 x 是等价无穷小． 即 sin x ~ x (x  0). 例如, 为 称 是 的主要部分． 定理 与 是等价无穷小的的充分 必要条件          ( ). 1 o (3 ) lim 0. 3 o x x 因此  0. 1. (1) (2)

注：并非任何两个无穷小都可以比较。例当x→+8 时1sin x都是无穷小量f(x)=g(x)xxg(x)但 lim:lim sinx不存在且不为无穷大f(x)x-→+ox-→+80故当 x→+oo 时 f(x)和g(x)不能比较。高等数学（上册）

例当 x   时 , 1 ( ) x f x  x x g x sin ( )  都是无穷小量 但   ( ) ( ) lim f x g x x x x lim sin  不存在且不为无穷大 故当 x   时 f ( x)和g( x)不能比较. 注：并非任何两个无穷小都可以比较

例1 证明：当x→0时,tanx－sinx为x的三阶无穷小tan x -sin x解··limt3x-→0sin x1-cosxlinx-→0xcosx1sinx11cosxlim= limlim2’x→0x-→0x-0 cos xx.tanx一sinx为x的三阶无穷小店高等数学（上册）

例1 证明 :当x  0时,tan x  sin x为x的三阶无穷小. 解 3 0 tan sin lim x x x x    ) sin 1 cos cos 1 lim( 2 0 x x x x x x      , 2 1  tan x  sin x为x的三阶无穷小. 2 0 0 0 1 cos lim sin lim cos 1 lim x x x x x x x x       

定理1β与α是等价无穷小的的充分必要条件为β=α+o(α).称α是β的主要部分，意义：用等价无穷小可给出函数的近似表达式例如，当x→0时,sinx ~ x,1-cosx ~21七2sin x = x + o(x)1-cosx=y=1cos.x2常用等价无穷小：当x→0时，x~sinx~tanx~arcsinx~arctanx~ln(1+x)~e*-11(1+x)k-1~kx(k0)1-cosx~2x/1+x-1~=(x→0)1+x-1~a-l~xlna(a>0,a±l)2中高等数学（上册）

意义：用等价无穷小可给出函数的近似表达式． 例如, sin x  x  o(x), ( ). 2 1 1 cos 2 2  x  x  o x 当x  0时, y  1  cos x 2 2 1 y  x 常用等价无穷小： 当x  0时, 2 ~ sin ~ tan ~ arcsin ~ arctan ~ ln(1 ) ~ 1, 1 1 cos ~ , (1 ) 1~ ( 0), 2 1~ ln ( 0, 1) x k x x x x x x x e x x x kx k a x a a a          . 2 1 sin ~ , 1 cos ~ 2 x x  x x 为 称 是 的主要部分． 定理 与 是等价无穷小的的充分 必要条件          ( ). 1 o

常用等价无穷小：当x→0时，x~ sin x ~ tan x ~arcsin x ~ arctan x~ ln(1+ x)~e -1,12(1+x)*-1~ kx(k0)1-cosx~2x/1+x-1~=(x→0)V1+x-1~2a-l~xlna(a>0,al)n再次验证上节课的内容：tan xarcsin xI-cosx求 lim求lim求lim2x-0x-0xxx-→0-1e'ln(1 + x)求 lim求 limx0x-0xx高等数学（上册）

再次验证上节课的内容： 0 ln(1 ) lim ; x x  x  求 0 1 lim . x x e  x 求 常用等价无穷小： 当x  0时, 2 ~ sin ~ tan ~ arcsin ~ arctan ~ ln(1 ) ~ 1, 1 1 cos ~ , (1 ) 1~ ( 0), 2 1~ ln ( 0, 1) x k x x x x x x x e x x x kx k a x a a a          0 tan lim ; x x  x 求 0 arcsin lim ; x x  x 求 2 0 1 cos lim ; x x  x  求

tan xo1o求 lim型x-0x1sin x解?原式=limx-0xcos x1sinxlim1m=1.1=1x→0x→0xcosxtanx所以,limx-→0x(x→0)tanx ~ x高等数学（上册）

0 tan lim . x x  x 求 0 sin 1 lim cos x x  x x 解 原式  0 0 sin 1 lim lim c o s x x x  x  x  111 tan x  x (x  0) 0 tan lim =1 x x  x 所以

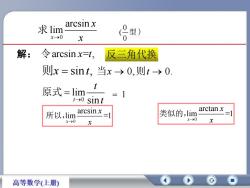
arcsin x求 lim型）x-00x解：令arcsin x=t,反三角代换则x=sint, 当x→0,则t→0.t原式=limt-→0 sintarctan xarcsinx类似的,lim所以,limx-→0xx→0x高等数学（上册）

0 arcsin lim =1 x x  x 所以， 0 arcsin lim x x  x 求 0 ( 0 型 ) 解： 令arcsin x=t, 则x  sin t, 0 lim t sin t  t 原式   1 当x  0,则t  0. 反三角代换 0 arctan lim =1 x x  x 类似的