《高等数学》课程教学资源（课件讲稿）第三章_3.4.3

第五节函数的极值与最大值最小值最大值最小值问题作业小结思考题第三章 微分中值定理与导数的应用高等数学（上册）

1 小结 思考题 作业 最大值最小值问题 第五节 函数的极值与 最大值最小值 第三章 微分中值定理与导数的应用

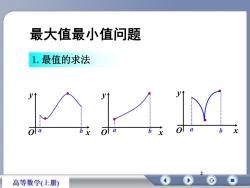
最大值最小值问题1.最值的求法olabaxabolh0xx高等数学（上册）

2 a b a b a b 最大值最小值问题 1.最值的求法 x y O x y O x y O

函数的最值1.闭区间上函数的最值步骤若函数f(x)在闭区间[a,b]上连续(1)求出函数所有可能极值点：驻点和导数不存在的点；(2)求出函数在驻点、导数不存在的点和区间端点的函数值：(3)比较这些函数值的大小，最大者即最大值，最小者即最小值2.实际应用中的最值实际问题中，若函数f(x）的定义域是开区间，且在开区间内有唯一驻点xo：根据实际问题可知最值必定存在，则唯一驻点即为最值点高等数学（上册）

函数的最值 1. 闭区间上函数的最值 2. 实际应用中的最值 0 实际问题中，若函数f (x) 的定义域是开区间，且在开区间内有唯一驻点x , 根据实际问题可知最值必定存在，则唯一驻点即为最值点. (1)求出函数所有可能极值点：驻点和导数不存在的点； (2)求出函数在驻点、导数不存在的点和区间端点的函数值； (3)比较这些函数值的大小，最大者即最大值，最小者即最小值. 步骤: 若函数f (x)在闭区间[a,b]上连续

2.应用举例例1求函数V=2x3+3x2-12x+14的在[-3.41上的最大值与最小值解 : f'(x) = 6(x + 2)(x -1)解方程 f'(x)=0,得 xi =-2,x, =1.计算f(-3)=23;f(-2) =34;f(1) =7;f(4) =142;y=2x+3x2-12x+14比较得最大值f(4)=142，最小值 f(1)= 7.高等数学（上册）

例1 解 f ( x)  6( x  2)(x  1) 3 2 求函数 y  2x  3x 12x 14的在[3, 4]上的最大值与最小值. 解方程 f ( x)  0,得 2, 1. x1   x2  计算 f (3)  23; f (2)  34; f (1) 7; f (4) 142; 比较得 最大值 f (4)  142， 最小值 f (1)  7. 2 3 12 14 3 2 y  x  x  x  2. 应用举例

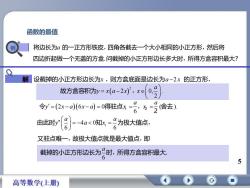
函数的最值将边长为α的一正方形铁皮，四角各截去一个大小相同的小正方形，然后将R四边折起做一个无盖的方盒.问截掉的小正方形边长多大时，所得方盒容积最大？福解设截掉的小正方形边长为x，则方盒底面是边长为α-2x的正方形故方盒容积为y=x(a-2x)，xe[0.号)2aa(舍去)令y=(2x-a)(6x-a)=0得驻点x-2N6-4α<0知x=~为极大值点，由此时y6又驻点唯一，故极大值点就是最大值点，即截掉的小正方形边长为一时，所得方盒容积最大，65高等数学（上册）

函数的最值 5 将边长为a 的一正方形铁皮，四角各截去一个大小相同的小正方形，然后将 四边折起做一个无盖的方盒.问截掉的小正方形边长多大时，所得方盒容积最大？ 设截掉的小正方形边长为x ，则方盒底面是边长为a 2 x 的正方形，   2 2 0, . 2 a y x a x x         故方盒容积为 ，    1 2 6 0 ( ). 6 a a 令y   x  a x  a  得驻点x  ，x2  舍去 2 又驻点唯一，故极大值点就是最大值点，即 1 4 0 6 6 a a y a x           由此时 知 为极大值点， 6 a 截掉的小正方形边长为 时，所得方盒容积最大. 例 解

例敌人乘汽车从河的北岸A处以1公里/分的速度向正北逃窜，同时我军摩托车从河的南岸B处向正东追击，速度为2公里/分．问我军摩托车何时射击最好（相距最近射击最好）？北解(1)建立敌我相距函数关系St设t为我军从B处发起东西0.5公里追击至射击的时间(分)B4公里敌我相距函数 s(t)南s(t) = (0.5 +1·t)2 +(4-2·t)高等数学（上册）

例 敌人乘汽车从河的北岸A处以1公里/分的速 度向正北逃窜，同时我军摩托车从河的南岸B处 向正东追击，速度为2公里/分．问我军摩托车何 时射击最好（相距最近射击最好）？ 北 南 西 东 解 建立敌我相距函数关系 追击至射击的时间 (分). 设 t 为我军从B处发起 敌我相距函数 2 2 s(t)  (0.5  1 t)  (4  2 t) s(t) (1) 0.5公里 4公里  A B  s(t)

s(t) = /(0.5 + t)2 + (4 - 2t)北st(2)求s=s(t)的最小值点东西 0.5公里。5t 7.5s'(t) =BT(0.5 + t)* + (4 - 2t)24公里南令s(t)=0,得唯一驻点 t=1.5，代入得 s(1.5)=V5显然不可导点t=-0.5(舍),t=2，s(2)=V/6.25故得我军从B处发起追击后1.5分钟射击最好高等数学（上册）

2 2 s(t)  (0.5  t)  (4  2t) (2) 求s  s(t)的最小值点. s(t)  . (0.5 ) (4 2 ) 5 7.5 2 2 t t t     令s (t)  0, 得唯一驻点 t 1.5, 故得我军从B处发起追击后1.5 分钟射击最好. 北 南 西 0.5公里 东 4公里  A B  s(t) t  0.5(舍),t  2, 代入得 s(1.5)  5. s(2)  6.25

函教的极值与最大值最大值三、小结极值：局部性概念；极值与最值的区别最值：整体性概念极大值可能小于极小值，极小值可能大于极大值函数的极值必在驻点和导数不存在的点取得第一充分条件；(合适选择好用极值的判别法第二充分条件哪个充分条件可简化计算、注意使用条件)实际问题求最值的步骤高等数学（上册）

8 三、小结 函数的极值与最大值最大值 极大值可能小于极小值, 函数的极值必在驻点和导数不存在的点取得. 极值的判别法 第一充分条件; (合适选择好用 极值:局部性概念; 极小值可能大于极大值. 极值与最值的区别 最值: 整体性概念. 实际问题求最值的步骤. 第二充分条件,       哪个充分条件可简化计算、注意使用条件)