《高等数学》课程教学资源（课件讲稿）第四章_4.1

第一节不定积分的概念与性质原函数与不定积分的概念「m不定积分的几何意义限基本积分表四、不定积分的性质五、小结思考题高等数学（上册）

一 、原函数与不定积分的概念 四、不定积分的性质 三、基本积分表 五、小结 思考题 第一节 不定积分的概念与性质 二、不定积分的几何意义

一、原函数与不定积分的概念定义如果在区间I内，可导函数F(x)的导函数为f(x),即VxEI，都有F(x)=f(x)或dF(x)= f(x)dx，那么函数F(x)就称为f(x)或f(x)dx在区间I内原函数.primitive function例 (sinx)sinx是cosx的原函数=cox(lnx) = 1lnx是二在区间(0,+o)内的原函数(x>0)xx原函数的概念：F'(x)= f(x)高等数学（上册）

例 sin x  cos x  sin x是cos x的原函数.   ( 0) 1 ln    x x x ln x是 x 1 在区间(0,)内的原函数. 定义： 如果在区间I 内，可导函数F( x)的 即x  I ，都有F ( x)  f ( x) 那么函数F( x)就称为 f ( x) 导函数为 f ( x)， 一、原函数与不定积分的概念 ( primitive function ) 定义 原函数的概念：F(x)  f (x)

含有第一类间断点的函数都没有原函数但是有第二类间断点的函数可能有原函数定理原函数存在定理：如果函数f(x)在区间I内连续，那么在区间I内存在可导函数F(x)：使Vx EI，都有F'(x)= f(x)简言之：连续函数一定有原函数问题：(1)原函数是否唯一？(2)若不唯一它们之间有什么联系?例(sin x)= cos x(sinx+C) = cosx（C为任意常数）高等数学（上册）

原函数存在定理： 如果函数 f ( x)在区间I 内连续， 简言之：连续函数一定有原函数. 问题：(1) 原函数是否唯一？ 例 sin x  cos x  sin x C  cos x   （C为任意常数） 那么在区间I 内存在可导函数F( x)， 使x  I，都有F(x)  f (x). (2) 若不唯一它们之间有什么联系？ 定理 含有第一类间断点的函数都没有原函数

关于原函数的说明：(1）若F(x)=f(x)，则对于任意常数C，F(x)+C都是f(x)的原函数(2）若F(x) 和G(x)都是 f(x)的原函数，则F(x)-G(x)=C（C为任意常数)证 ：: [F(x)-G(x)} =F(x)-G(x)= f(x)-f(x)= 0（C为任意常数）F(x)-G(x)=C说明F(x)+c是f(x)的全部原函数高等数学（上册）

关于原函数的说明： （1）若F(x)  f (x) ，则对于任意常数 C ， F(x)  C都是 f (x)的原函数. （2）若F(x) 和G( x)都是 f (x) 的原函数， 则 F(x) G(x)  C （C为任意常数） 证 F(x) G(x)  F(x)  G(x)     f (x)  f (x)  0  F(x)  G(x)  C （C为任意常数） 说明Fx c是f x的全部原函数

定义不定积分(indefiniteintegral)的定义：在区间I内，函数f(x)的带有任意常数项的原函数称为f(x)在区间I内的不定积分，记为「f(x)dxF(x)+Cf(x)dx三被积表达式任意常数被积函数原函数积分号积分变量高等数学（上册）

任 意 常 数 积 分 号 被 积 函 数 不定积分(indefinite integral)的定义： 在区间I内， f (x)dx  F(x)  C  被 积 表 达 式 积 分 变 量 函数 f (x)的带有任意 常数项的原函数 称为 f (x)在区间I内的 不定积分，记为 f (x)dx. 定义 原 函 数

(?)= xsx'dx.例1 求.6x+解x:661求例2 dx.1 + x2解：(arctan2--1dx = arctan x + C.高等数学（上册）

例1 求 5 x dx.  解 , 6 5 6 x x          6 5 6 d . x  x x   C  解 例2 求 2 1 1 dx.  x    , 1 1 arctan 2 x x     2 1 1 dx arctan x C. x     

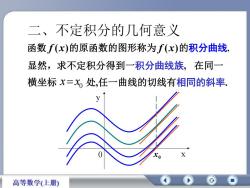
不定积分的几何意义二函数f(x)的原函数的图形称为f(x)的积分曲线在同一显然，求不定积分得到一积分曲线族横坐标x=处,任一曲线的切线有相同的斜率V0Xx0高等数学（上册）

二、不定积分的几何意义 函数 f (x)的原函数的图形称为 f (x)的积分曲线. 显然，求不定积分得到一积分曲线族, 横坐标 处,任一曲线的切线有相同的斜率. 0 xx 0 x y 0 x 在同一

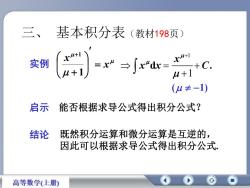
基本积分表（教材198页）一ru+1xu+1实例ru+C=dxμ+1+(u ± -1)启示能否根据求导公式得出积分公式？结论既然积分运算和微分运算是互逆的，因此可以根据求导公式得出积分公式高等数学（上册）

实例    x x           1 1 1 1 d . x x x C          启示 能否根据求导公式得出积分公式？ 结论 既然积分运算和微分运算是互逆的， 因此可以根据求导公式得出积分公式. (  1) 三、 基本积分表（教材198页）

基本积分表☆kdx = kx +C(k是常数);(1)ru+1C2'du±-1):μ+1dx(3)= ln+CX(4)Ix = arctan x + C:(5)dx = arcsin x + C:2(6)cos xdx = sin x + C;(7)sin xdx =- cosx + C:高等数学（上册）

基 本 积 分 表  (1) kdx  kx C (k  是常数); 1 2 1 1 ( ) d ( ); x x x C            3 d ( ) ln ; x x C x    2 1 1 1 2 dx C x x dx x C x        2 1 4 1 ( ) dx x    arctan x  C; 2 1 5 1 ( ) dx x    arcsin x  C; (6) cos xdx   sin x  C; (7) sin xdx    cos x  C;

dx(8)sec? xdx =tan x + C;cos' xdx(9)[ csc? xdx =-cot x + C;sin?(10)sec xtan xdx = sec x + C;(11)I csc xcot xdx =- csc x +C;(12)[e*dx =e* +C;qt(13)a'dx+C;Ina高等数学（上册）

(10) sec xtan xdx   sec x  C; (11) csc xcot xdx    csc x  C; (12) d x e x   e C; x  (13) d x a x   ; ln C a a x  2 8 d ( ) cos x x   2 sec xdx   tan x  C; 2 9 d ( ) sin x x   2 csc xdx    cot x  C;