《高等数学》课程教学资源（课件讲稿）第三章课件_第三章第五节

第五节第三章函数的极值与最大值最小值函数的极值及其求法一、最大值与最小值问题HIGH EDUCATION PRESS机动目录上页下页返回结束

二、最大值与最小值问题 一、函数的极值及其求法 第五节 机动 目录 上页 下页 返回 结束 函数的极值与 最大值最小值 第三章

一、函数的极值1、定义:设函数 f(x)在(a,b)内有定义，xo E(a,b)若存在xo的一个邻域，在其中当x≠xo 时，(1)f(x)f(xo),则称 xo为 f(x)的极小点称f(xo）为函数的极小值极大点与极小点统称为极值点HIGH EDUCATIONPRESS机动目录上页下页返回结束

一、函数的极值 1、定义: 在其中当 时, (1) 则称 为 的极大点 , 称 为函数的极大值 ; (2) 则称 为 的极小点 , 称 为函数的极小值 . 极大点与极小点统称为极值点 . 机动 目录 上页 下页 返回 结束

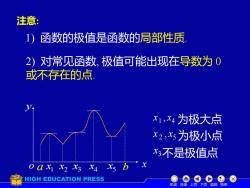
注意：函数的极值是函数的局部性质D2）对常见函数极值可能出现在导数为0或不存在的点为极大点X1,X4为极小点X2,X5x3不是极值点o axxx xx bxHIGHEDUCATIONPRESS机动目录上页下页返回结束

注意: x1 x3 4 x 2 x x5 x o a b y 1 4 x , x 为极大点 2 5 x , x 为极小点 3 x 不是极值点 2) 对常见函数, 极值可能出现在导数为 0 或不存在的点. 1) 函数的极值是函数的局部性质. 机动 目录 上页 下页 返回 结束

2、极值存在的必要条件若可导函数y=f(x)在点x取得极值,则点x一定是其驻点，即f(x）=0HIGHEDUCATION PRESS

2、极值存在的必要条件

极值存在的第一充分条件3、U(x,8)内可导设函数(x）在x处连续，且在x的某去心邻域(1)若 xE (x。-S,x) 时, f'(x)> 0,f(x）在x处取得极大值；x e (xo,x。+8) 时, f(x) 0,(3)若xEU(xoS）时，f(x)的符号保持不变则f(x）在x处没有极值HIGH EDUCATIONPRESS

(1)若 0 0 x x x  − ( , )  时， f x ( ) 0,  0 0 x x x  + ( , )  时， f x ( ) 0,  f x( ) 在 x0 处取得极大值； (2)若 0 0 x x x  − ( , )  时， f x ( ) 0,  0 0 x x x  + ( , )  时， f x ( ) 0,  f x( ) 在 x0 处取得极小值； (3)若 0 ( , ) o x U x   时， f x ( ) 的符号保持不变, 则 f x( ) 在 x0 处没有极值 设函数f(x)在x0处连续，且在x0的某去心邻域 0 ( , ) o U x  内可导. 3、极值存在的第一充分条件

例.求函数的极值f(x)=(x-1)x3解:1)求导数r(x)=x3+(x-1)x-=最2）求极值可能点导数不存在的点 x2 = 0f'(x)=0，得xi=3)列表判别NIL-818一X0f(x)3/20f(x)25J f(0)=0.x=0是极大点,其极大值为33/20是极小点，其极小值为f()=X=5HIGH EDUCATION PRESS机动目录上页下页返回结束

例. 求函数 的极值 . 解:1) 求导数  = +3 2 f (x) x 3 1 3 2 ( 1) − x −  x 3 5 2 3 x x − = 2) 求极值可能点 f (x) = 0 , 得 ; 5 2 x1 = 导数不存在的点 0 x2 = 3) 列表判别 x f (x) f (x)  0 5 2 0 + − + 0 3 3 20 25 − (− , 0) (0 , ) 5 2 ( , ) 5 2 +  是极大点，其极大值为 是极小点，其极小值为 机动 目录 上页 下页 返回 结束

f"(xo)极值存在的第二充分条件f'(x)- f'(xo)lim二设函数f(x)在xo处具有二阶导数x→XOX-Xo且f'(xo)=0,f"(xo)±0,f'(x)= limx→xo X-Xo(1)当 f"(xo)0 时,函数f(x)在xo处取得极小值(3)当f"(xo）=0时,函数f(x)在xo处有可能取得极值，也有可能不是极值HIGHEDUCATIONPRESS

4、极值存在的第二充分条件 设函数f (x)在x0处具有二阶导数 且 f '(x0 )=0, f "(x0 )≠0, (1)当 f "(x0 )0 时, 函数 f (x) 在 x0 处取得极小值. (3) 当 f "(x0 ) =0 时, 函数 f (x)在 x0 处 有可能取得极值，也有可能不是极值 ( ) 0 f  x 0 0 ( ) ( ) lim 0 x x f x f x x x −  −  = → 0 ( ) lim 0 x x f x x x −  = →

例. 求函数 f(x)=(x2-1)3 +1的极值解：1）求导数f'(x)= 6x(x2 -1)2, f"(x)= 6(x2 -1)(5x2 -1)2)求驻点令f(x)=0，得驻点x =-1,x2=0,×=13) 判别因f"(0)=6>0,故f(0)=0为极小值又f"(-1)=f"(1)=0,故需用第一判别法判别由于f(x)在x=±1左右邻域内不变号::f(x)在x=±1没有极值HIGH EDUCATION PRESS机动目录上页下页返回结束

例. 求函数 的极值 . 解: 1) 求导数 ( ) 6 ( 1) , 2 2 f  x = x x − ( ) 6 ( 1) (5 1) 2 2 f  x = x − x − 2) 求驻点 令 f (x) = 0 , 得驻点 1, 0 , 1 x1 = − x2 = x3 = 3) 判别 因 f (0) = 6  0 , 故 为极小值 ; 又 f (−1) = f (1) = 0 , 故需用第一判别法判别. 1 x y −1 机动 目录 上页 下页 返回 结束

判别法的推广若函数f(x)在xo点有直到 n阶导数f'(xo)= f"(xo)=...= f(n-1)(xo)=0, f(")(x。)* 01）当n为偶数时，x.为极值点f(n)(xo)>0时，Xo是极小点;f(n)(xo)<0时，Xo是极大点2）当n为奇数时，x.不是极值点HIGH EDUCATION PRESS机动目录上页下页返回结束

判别法的推广 ( ) 0 , 0 ( ) f x  n 1) 当 n 为偶数时, 是极小点 ; 是极大点 . 2) 当 n 为奇数时, 为极值点 , 不是极值点 . 机动 目录 上页 下页 返回 结束

三、函数的最值若函数 f(x)在闭区间[a,b]上连续则其最值只能在极值点或端点处达到求函数最值的方法：(1）求出f(x)在（a,b)内的驻点和不可导点(2)计算f(x)在上述驻点、不可导点处的函数值及 f(a), (b);最大者为最大值(3）上述函数值中，最小者为最小值HIGH EDUCATION PRESS机动目录上页下页返回结束

三、函数的最值 则其最值只能在极值点或端点处达到 . 求函数最值的方法: 机动 目录 上页 下页 返回 结束 (1) 求出 f (x) 在 (a,b) 内的驻点和不可导点; (2) 计算 f (x) 在上述驻点、不可导点处的函数值 及 f(a), f(b); (3) 上述函数值中，最大者为最大值， 最小者为最小值