《高等数学》课程教学资源（课件讲稿）第二章课件_第二章第五节

第二章第五节函数的微分一、微分的定义二、微分的几何意义三、微分的计算与应用HIGH EDUCATION PRESS机动目录上页返回下页结束

第五节 机动 目录 上页 下页 返回 结束 函数的微分 第二章 一、微分的定义 二、微分的几何意义 三、微分的计算与应用

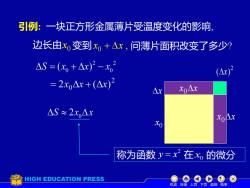
引例：一块正方形金属薄片受温度变化的影响边长由xo变到xo+△x，问薄片面积改变了多少？△S = (x。 + △x)? - xo(x)= 2xoAx +(△x)XoAxAx△S ~ 2xo△xXoAxXo称为函数y=x在x。的微分HIGH EDUCATION PRESS机动目录上页下页返回结束

引例: 一块正方形金属薄片受温度变化的影响, 问薄片面积改变了多少? 0 x x x x 0 x x 0 2 (x) 称为函数 0 x 变到 , 0 边长由 x + x 机动 目录 上页 下页 返回 结束 2 y x = 在 x0 的微分

一、定义：若函数y=_f(x)在点 xo 的增量可表示为△ y= f(xo + △x)- f(xo) = A△x +o(△x)(A为不依赖于Ax的常数）则称函数 =f(x)在点xo可微A△x称为f(x)在 点xo的微分记作dy或df即dy = AxHIGH EDUCATION PRESS机动目录上页下页返回结束

的微分 一、定义: 若函数 在点 x0 的增量可表示为 ( A 为不依赖于△x 的常数) 则称函数 y = f (x) 称为 记作 即 dy = Ax = Ax + o(x) 在点 可微 机动 目录 上页 下页 返回 结束 A x

定理：函数V=f(x）在点xo可微的充要条件是= f(x)在点 xo处可导, 且 A=f(xo)即 dy= f'(xo)△x证：“必要性”已知 y=f(x)在点xo可微,则 y= f(xo +△x) - f(xo) = Ax +o(△x)o(△x)A= lim(A+limxAx-→0 △xAx-0故y=f(x)在点xo的可导,且f(xo）=AHIGH EDUCATION PRESS机动目录上页下页返回结束

定理 : 函数 证: “必要性” 已知 在点 可微 , 则 ( ) ( ) 0 0  y = f x + x − f x ) ( ) lim lim ( 0 0 x o x A x y x x   = +     →  → = A 故 = Ax + o(x) 在点 的可导, 且 在点 x0 可微的充要条件是 在点 处可导, 且 即 dy = f (x )x 0 机动 目录 上页 下页 返回 结束

定理：函数=f（x）在点xo可微的充要条件是y= f(x) 在点xo处可导, 且 A= f(x)即 dy= f'(xo)△x已知 y=f(x)在点 xo的可导“充分性Ay= f'(xo)limAr-→0 △xAy=f'(xo)+α（ lim α=0)△x△x-0故 Ay= f'(xo)△x +α△x = f'(xo)Ax+o(△x)即 dy= f'(xo)△xHIGH EDUCATION PRESS机动目录上页下页返回结束

定理 : 函数 在点 x0 可微的充要条件是 在点 处可导, 且 即 dy = f (x )x 0 “充分性” 已知 lim ( ) 0 0 f x x y x =     → =  +    ( ) 0 f x x y ( lim 0 ) 0 =  →  x y = f (x )x +x 故 0 ( ) ( ) 0 = f  x x + o x 即 dy = f (x )x 0 在点 的可导, 机动 目录 上页 下页 返回 结束

例. 求y=x3,在 x=1时,△x分别等于0.01和0.02时的增量与微分y = arctanxda十AHIGHEDUCATION PRESS机动目录上页下页返回结束

例. 机动 目录 上页 下页 返回 结束 3 y x x , 1 x = =  求 在 时， 分别等于0.01和0.02时的增量与微分 y = arctan x , dy x x d 1 1 2 + =

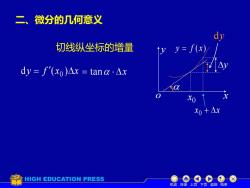
二、行微分的几何意义切线纵坐标的增量y= f(x)dy = f'(xo)△x = tanα △xHXoXo + xHIGHEDUCATION PRESS机动目录上页下页返回结束

二、微分的几何意义 dy = f (x )x 0 x + x 0 x y o y = f ( x)  0 x y dy = tan  x 切线纵坐标的增量 机动 目录 上页 下页 返回 结束

三、微分运算法则设u(x),v(x)均可微，则2. d(Cu) = Cdu(C为常数)1. d(u ±v)= du± dyvdu-udy3. d(uv) = vdu + udy4. d(=)V￥(05.复合函数的微分y=f(u),u=p(x)分别可微则复合函数 y=f[β(x)]的微分为dudy = yx dx = f'(u)@'(x)dxdy = f'(u)du微分形式不变HIGH EDUCATION PRESS机动目录上页下页返回结束

三、 微分运算法则 设 u(x) , v(x) 均可微 , 则 (C 为常数) 分别可微 , 的微分为 = f (u)(x) dx du dy = f (u) du 微分形式不变 5. 复合函数的微分 则复合函数 = du  dv = vdu + udv 机动 目录 上页 下页 返回 结束

例. y= ln(1 +e*"),求 dy.解：d(l+e)dyerd(x)O1f2xdxe2xe*dxHIGHEDUCATION PRESS机动目录上页下页返回结束

例. 求 解: 2 1 1 d x e y + = d(1 ) 2 x + e  + = 2 1 1 x e d ( ) 2 x e x x e x x 2 d 1 1 2 2   + = x e xe x x d 1 2 2 2 + = 2 x e 机动 目录 上页 下页 返回 结束

微分在近似计算中的应用△y = f'(xo)△x +o(△x)当△x|很小时，得近似等式Ay= f(xo +△x)- f(xo) ~ f'(xo)Axf(xo +△x) = f(xo)+ f'(xo)△x令 x = Xo + △xf(x) = f(xo)+ f(xo)(x - xo使用原则：：1)f(xo),f'(xo)好算;2）x与xo靠近，HIGH EDUCATION PRESS机动目录上页下页返回结束

微分在近似计算中的应用 ( ) ( ) 0  y = f  x x + o x 当 x 很小时, ( ) ( ) 0 0  y = f x + x − f x  f (x )x 0 f (x + x)  f (x ) + f (x )x 0 0 0 x = x + x 令 0 使用原则: 1) ( ), ( ) ; f x0 f  x0 好算 2) . x 与x0 靠近 ( ) ( ) ( )( ) 0 0 0 f x  f x + f  x x − x 得近似等式: 机动 目录 上页 下页 返回 结束