《高等数学》课程教学资源（课件讲稿）第三章课件_第三章第六节

第三章第六节函数图形的描绘HIGHEDUCATION PRESS机动目录上页返回下页结束

第六节 机动 目录 上页 下页 返回 结束 函数图形的描绘 第三章

函数图形的描绘一、步骤：1. 确定函数 y=f(x)的定义域,并考察其奇偶性及周期性;2. 求f'(x)，,f"(x),并求出f'(x)及f"(x)为 0 和不存在的点;3.列表判别增减及凹凸区间，求出极值和拐点：4. 求水平、铅直渐近线5.确定某些特殊点，描绘函数图形HIGHEDUCATIONPRESS机动目录上页下页返回结束

一、函数图形的描绘 步骤 : 1. 确定函数 的定义域 , 期性 ; 2. 求 并求出 及 3. 列表判别增减及凹凸区间 , 求出极值和拐点 ; 4. 求水平、铅直渐近线 ; 5. 确定某些特殊点 , 描绘函数图形 . 为 0 和不存在 的点 ; 并考察其奇偶性及周 机动 目录 上页 下页 返回 结束

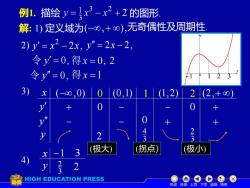
例1.描绘=↓x3-x2+2的图形解：1)定义域为(-0,+00),无奇偶性及周期性2) y'=x2 -2x, y"=2x -2令y'=0,得x=0,2令y"=0,得x=13)x(-8,0)102(2,+8)1(0.1111(1.2)7000V4-32-3V2(拐点)(极大)(极小)3-X213V2HIGH EDUCATION PRESS机动目录上页下页返回结束

例1. 描绘 的图形. 解: 1) 定义域为 无奇偶性及周期性. 2) 2 , 2 y  = x − x y  = 2x − 2, 令 y  = 0, 令 y  = 0, 3) x y  y  y (−,0) 0 (0,1) 1 (1,2) 2 (2,+ ) + 0 − − 0 + − − + + 2 3 4 (极大) (拐点） 3 2 (极小) 4) x y −1 3 3 2 2 0 机动 目录 上页 下页 返回 结束 −1 1 2 3

例2.描绘函数的图形解：1)定义域为(-00,+80),图图形对称于y轴2)求关键点L元令y'=0得x=0；令y"=0得x=±11(0, 1)(1. +8)0x3）判别曲线形态V中2元e（拐点）(极大)DHIGHEDUCATION PRESS机动目录上页下页返回结束

例2. 描绘函数 的图形. 解: 1) 定义域为 图形对称于 y 轴. 2) 求关键点 y  = 2 1 − , 2 2 x x e − y  = 2 1 − 2 2 x e − (1 ) 2 − x 令 y  = 0得 x = 0; 令 y  = 0得x = 1 机动 目录 上页 下页 返回 结束 − − − + 2 1 0 0 2 e 1 x y  y  y 0 (0, 1) 1 (1, + ) 3) 判别曲线形态 (极大) (拐点)

1(0,1)(1, +8)0xy2元e(极大)(拐点）4)求渐近线Vlim y= 02元x80B：y=0为水平渐近线x5) 作图HIGH EDUCATION PRESS机动目录上页下页返回结束

(极大) (拐点) lim = 0 → y x  y = 0 为水平渐近线 5) 作图 4) 求渐近线 机动 目录 上页 下页 返回 结束 − − − + 2 1 0 0 2 e 1 x y  y  y 0 (0, 1) 1 (1, + ) 2 2 2 1 x y e − =  x y o A B 2 1

例3.描绘方程(x-3)＋4-4x=0的图形(x-3)解: 1) :定义域为(一80,1),(1,+0+4(x-1)2)求关键点2(x -3) +4y'- 4y- 4xy'= 0y'=x-3-2y _ (x-3)(x+1)2(x -1)4(x-1)22+4y"-8y'-4xy"= 01-4y'2(x-1)(x-1)令y'=0得 x=-1,3;HIGH EDUCATION PRESS机动目录上页下页返回结束

例3. 描绘方程 的图形. 解: 1) , 4( 1) ( 3) 2 − − = x x y 定义域为 2) 求关键点  2(x − 3) + 4 y − 4 y − 4xy  = 0 2( 1) 3 2 − − −   = x x y y  2 + 4 y − 8 y  − 4xy  = 0 2( 1) 1 4 − −    = x y y 令 y  = 0得 x = −1, 3 ; 机动 目录 上页 下页 返回 结束

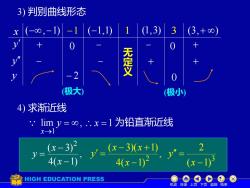
3）判别曲线形态3(1,3)(-1.1)1(3,+00)无定义(极大)(极小)4)求渐近线lim y=8，x=1为铅直渐近线x→1(x-3)2(x -3)(x +1)V=(x-1)34(x-1)4(x-1)2HIGH EDUCATION PRESS机动目录上页下页返回结束

x (−,−1) −1 (−1,1) 1 (1,3) 3 (3,+ ) y  y  y + − − + − − + + − 2 0 , 4( 1) ( 3) 2 − − = x x y , 4( 1) ( 3)( 1) 2 − − +  = x x x y 3 ( 1) 2 −  = x y 3) 判别曲线形态 0 0 (极大) (极小) 4) 求渐近线 lim , 1 =  → y x  为铅直渐近线 无 定 义 机动 目录 上页 下页 返回 结束 x =1

D又因lim即k=x-00 x(x-3)limtb = limA4(x- 1)X80x→85-5x+9= lim(x-3)244(x-1)x00y=4(x- 1)为斜渐近线(x-3)(x+1)44(x-1)2x05）求特殊点229(x-1)44HIGH EDUCATION PRESS机动目录上页下页返回结束

又因 x y x→ lim , 4 1 = 4 1 即 k = ) 4 1 b lim ( y x x = − → ] 4 1 4( 1) ( 3) lim [ 2 x x x x − − − = → 4( 1) 5 9 lim − − + = → x x x 4 5 = − 4( 1) ( 3) 2 − − = x x y 5) 求特殊点 x y 0 4 9 − 2 4 1 为斜渐近线 4 5 4 1  y = x − 机动 目录 上页 下页 返回 结束 2 4( 1) ( 3)( 1) − − +  = x x x y 3 ( 1) 2 −  = x y

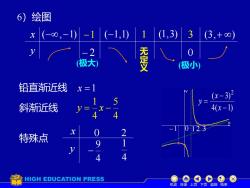
绘图6)3(1,3)(-8,-1)-1(-1,1)1(3, +00)无定义(极大)(极小)铅直渐近线x=(x-3)2V=4(x-1)斜渐近线0:12一x2O特殊点14HIGH EDUCATION PRESS机动目录上页下页返回结束

6）绘图 (极大) (极小) 斜渐近线 铅直渐近线 x =1 4 5 4 1 y = x − 特殊点 −1 0 12 3 4( 1) ( 3) 2 − − = x x y 机动 目录 上页 下页 返回 结束 − 2 无 定 义 x y (−,−1) −1 (−1,1) 1 (1,3) 3 (3,+ ) 0 x y 0 4 9 − 2 4 1