《高等数学》课程教学资源（课件讲稿）第三章课件_第三章第一节

第三章第一节微分中值定理一、罗尔(Rolle)定理二、拉格朗日中值定理三、柯西(Cauchy)中值定理HIGH EDUCATION PRESS机动目录上页返回下页结束

一、罗尔( Rolle )定理 第一节 机动 目录 上页 下页 返回 结束 二、拉格朗日中值定理 三、柯西(Cauchy)中值定理 微分中值定理 第三章

一、罗尔(Rolle)定理费马（fermat）引理y= f(x)在U(xo)有定义,>f(xo)= 0且f(x)≤f(xo), '(xo)存在(或≥)证: 设Vxo +△x U(xo), f(xo +△x)≤ f(xo)XXoCf(xo +x) - f(xo)则 f(xo)= limAxAx-→0f"(xo) ≥0 (△x→0-)>f(xo)= 0fi(xo)≤0 (△x -→0+)证毕HIGH EDUCATION PRESS费马目录上页下页返回结束

费马(fermat)引理 一、罗尔( Rolle )定理 且 存在 (或  ) 证: 设 则  0  0 x y o 0 x 费马 目录 上页 下页 返回 结束 证毕

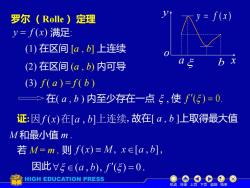
(y=f(x)罗尔（Rolle）定理y=f(x) 满足(1)在区间[α,b]上连续b xEO(2)在区间 (α,b) 内可导(3) f(a)=f(b)在(α,b)内至少存在一点 ,使 f（)=0证:因f(x)在[a,b]上连续,故在[a,b]上取得最大值M和最小值m若 M=m,则f(x)=M,xE[a,b]因此V(α,b), f'()=0,HIGH EDUCATION PRESS机动目录上页下页返回结束

罗尔（ Rolle ）定理 满足: (1) 在区间 [a , b] 上连续 (2) 在区间 (a , b) 内可导 (3) f ( a ) = f ( b ) 使 f ( ) = 0. x y o a b y = f ( x )  证: 故在[ a , b ]上取得最大值 M 和最小值 m . 若 M = m , 则 因此 在( a , b ) 内至少存在一点 机动 目录 上页 下页 返回 结束

若 M>m，则M和m中至少有一个与端点值不等不妨设 M ≠ f(a),则至少存在一点 E(a,b),使 f()= M,则由费马引理得 f'（）=0HIGHEDUCATION PRESS机动目录上页下页返回结束

若 M > m , 则 M 和 m 中至少有一个与端点值不等, 不妨设 则至少存在一点 使 则由费马引理得 f ( ) = 0. 机动 目录 上页 下页 返回 结束

说明：1）定理条件条件不全具备，结论不一定成立0≤x<1f (x)0x=1f(x)=[xlxe[-1,1]f(x)= x,xe[0,12）定理条件只是充分的f(x) = x ,x E[-1,2]HIGH EDUCATIONPRESS机动目录上页下页返回结束

说明: 1) 定理条件条件不全具备, 结论不一定成立. 1x y o 1x y −1 o 1x y o 机动 目录 上页 下页 返回 结束 2) 定理条件只是充分的

例. 设f(x)=(x-1)(x-2)(x-3)(x-4)不求导数证明方程f（x）有3个实根例.证明方程星x2-5x+3=0有且仅有一个小于1的正实根例.已知函数 f(x)在[0,a]上连续，在(O,a)内可导，且f(O)=f(a)=0,证明： 至少存在一点ε(0,a)使f'()-2f()=0HIGH EDUCATION PRESS机动目录上页下页返回结束

机动 目录 上页 下页 返回 结束 例. 证明方程 有且仅有一个小于1 的 正实根 . 设 不求导数 证明方程 有3个实根 例. 例

y= f(x)二、拉格朗日中值定理Vy=f(x）满足(l)在区间「α,bl上连续bx2Q(2)在区间（α,b）内可导至少存在一点 e(a,b),使 F()=T(b)-T(a)L7Vb-af(b)- f(a) = 0f(5)-J证：问题转化为证b-a0(x)= f(x) _ f(b)-f(a)作辅助函数b-aβ(x)在[a,b］上连续在（α,b）内可导bf(a)-af(b)= p(b)p(a)=b-aHIGH EDUCATION PRESS拉氏目录上页下页返回结束

二、拉格朗日中值定理  ( )   (1) 在区间 [ a , b ] 上连续 满足: (2) 在区间 ( a , b ) 内可导 至少存在一点 使 . ( ) ( ) ( ) b a f b f a f − −   =  x y o a b y = f ( x ) 作辅助函数 在 [ a , b ] 上连续 , 在 ( a , b ) 内可导, 证: 问题转化为证  ( x) = f (x) x b a f b f a − − − ( ) ( ) ( ) a = ( ) b b a b f a a f b − − = ( ) ( ) 拉氏 目录 上页 下页 返回 结束 0 ( ) ( ) ( ) = − −  − b a f b f a f 

拉格朗日中值定理的有限增量形式a=x,b=x+△x则 f(x+Ax)-f(x)= f'()Ax(介于x+△x与x之间(0<0<1)Ay= f'()Ax = f'(x + 0Ax)Ax△y= f'(xo)△x + o(△x)Ay = dy = f'(xo)Ax例.设 f(x)=3x2+2x+5求f(x)在[4,6]上满足拉日中值定理的HIGHEDUCATIONPRESS机动目录上页下页返回结束

拉格朗日中值定理的有限增量形式: ( ) 0  =  = +     y f x f x x x      ( ) (0 1) 令 则 (介于x x x +  与 之间) 机动 目录 上页 下页 返回 结束 ( ) ( ) 0  y = f  x x + o x 例. 设 0   =  y dy f x x ( )

定理：如果函数f(x）在区间「上连续,I内可导且导数恒为零,那么f(x）在区间「上是一个常数Xi,X2 (Xi <x2)证：在1上任取两点在[x,x,]上用拉日中值公式,得(xi<5<x2)f(x2)- f(x) = f'()(x2 -x)= 0f(x2)= f(xi)由xi,x2的任意性知，f(x)在上为常数推论：若在区间(a,b)上f'(x)=g(x)则在(a,b)上f(x)-g(x)=CHIGH EDUCATION PRESS机动目录上页下页返回结束

定理: 证: 在 I 上任取两点 = 0 由 的任意性知, 在 I 上为常数 . 机动 目录 上页 下页 返回 结束 推论：若在区间

元例.证明等式XE(-00, +80)arctan x + arccot x =福证：设则在(-80,+8)上f(x)=arctan x+arccot x1+x1 + x(常数)由推论可知f(x)= arctan x + arccot x = C元令 x = 1, 得 f(l)=arctanl+arccotl HIGH EDUCATION PRESS机动目录上页下页返回结束

例. 证明等式 证: 设 由推论可知 (常数) 令 x = 1, 得 arctan arc cot , x  − +  ( , ) 2 x x  + = 机动 目录 上页 下页 返回 结束