《高等数学》课程教学资源（课件讲稿）第二章_2.4

第五节函数的微分微分的定义-二.微分的几何意义三、基本初等函数的微分公式与微分运算法则四、微分在近似计算中的应用五、小结思考题高等数学（上册）

一、微分的定义 二、微分的几何意义 三、基本初等函数的微分公式 与微分运算法则 五、小结 思考题 第五节 函数的微分 四、微分在近似计算中的应用

一、微分的定义(differential)1.实例：正方形金属薄片受热后面积的改变量(△r)设边长由x.变到x。+△x，LAtAtAX：正方形面积A=x。，:. △A =(x。 + Ax)2 - x?A=xiXerA= 2x, ·Ax +(△x)2(1)(2)1)：△Ax的线性函数且为△A的主要部分2)：△的高阶无穷小当△x很小时可忽略高等数学（上册）

一、微分的定义(differential) 1.实例:正方形金属薄片受热后面积的改变量. 2 A  x0 0 x 0 x , 0 0 设边长由x 变到x  x , 2 正方形面积 A  x0 2 0 2 0 A  (x  x)  x 2 ( ) . 2 0  x  x  x (1) (2) x的线性函数,且为A的主要部分; x的高阶无穷小,当x很小时可忽略. (1): (2): x x 2 (x) x0x x0x

正方形面积A=x2A=(x.+Ax)2-x)再例如,设函数=x在点x,处的改变量= 2x, ·Ax+(Ax)(1)(2)为△x时，求函数的改变量Ay设函数y=rAy=(x, +Ax) -x,Ay =(x。 + Ax)3 - x)=3x,-Ax+3x, (Ar)*+(Ar)2= 3x? . Ax +3x, :(Ar)? +(x)3(1)(2)当△x很小时，(2)是△x的高阶无穷小o(△x)既容易计算又是较好的近似值:. Ay ~ 3x? . Ax.高等数学（上册）

再例如, , . 0 3 x y y x x    为 时 求函数的改变量 设函数 在点 处的改变量 3 0 3 0 y  (x  x)  x 3 3 ( ) ( ) . 2 3 0 2 0  x  x  x  x  x (1) (2) 当x很小时, 3 . 2 y  x0  x (2)是x的高阶无穷小o(x), 既容易计算又是较好的近似值

函数凡）在点x处可微：2.定义AAx+o(Ar)AV设函数y=f(x)在某区间内有定义微分dyx.及xo+△x在这区间内，如果正方形面积A=xM=(x。+Ar) -x)Ay = f(x + △x) - f(xo) = A·△x+o(△x)=2x,-Ar+(Ar)(2)成立(其中A是与△x无关的常数)，则称函数设函数y=xAy=(x,+Ax)-xy=f(x)在点x.可微，并且称A·△x为函数=3x,-Ar+3x, (Ar) +(Ar))2y=f(x)在点x.相应于自变量增量△x的微分记作dyx=x或df(x），即dyx=x。=A·△x.微分dy=f（x）Ax微分dy叫做函数增量△y的线性主部（微分的实质）高等数学（上册）

2. 定义 0 0 0 0 0 0 0 0 0 ( ) , , ( ) ( ) ( ), ( ) , ( ) , d d ( ), ( d . ) x x x x y f x x x x f x x f x x y f x A x y A x o x A x y f x x f y A x x y x                       设函数 在某区间内有定义 及 在这区间内 如果 成立 其中 是与 无关的常数 则称函数 在点 并且称 为函数 在点 相应于自变量 可 增量 分 微 的 或 即 微 记作 微分dy叫做函数增量y的线性主部. (微分的实质) 微分dy 微分dy  f (x)x

3.可微(differentiable)的条件定理函数f(x）在点x，可微的充要条件是函数f(x)在点x处可导, 且A=f"(xo).可导可微微分 dy = f'(x)△x通常把自变量x的增量△x称为自变量的微分记作dx，即dx=△x.微分就是导数微分dy= f'(x)dx与dx的乘积高等数学（上册）

3. 可微(differentiable)的条件 ( ) , ( ). ( ) 0 0 0 f x x A f x f x x 数 在点 处可导 且   定理 函数 在点 可微的充要条件是函 可导  可微. 微分dy  f (x)dx. , . , dx dx x x x    记作 即 通常把自变量 的增量 称为自变量的微分 微分dy  f (x)x

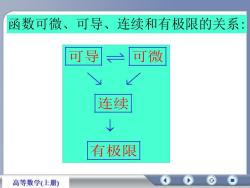
函数可微、可导、连续和有极限的关系可导可微连续有极限高等数学（上册）

函数可微、可导、连续和有极限的关系:     可导 可微 连续 有极限

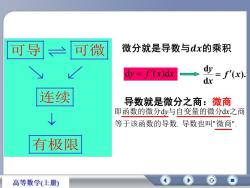
微分就是导数与dx的乘积可导可微dydy =f(x)dx.f'(x)dx连续导数就是微分之商：微商即函数的微分dy与自变量的微分dx之商等于该函数的导数，导数也叫"微商有极限高等数学（上册）

dy  f (x)dx. ( ). d d f x x y   d d . " ". 即函数的微分 y与自变量的微分 x之商 等于该函数的导数 导数也叫 微商 导数就是微分之商：微商     可导 可微 连续 有极限

例1求函数y=x3当x=2，△x=0.02时的微分解因为微分dy=f(x)dx= f(x)△x.: dy = (x3)△x = 3xAr= 3x△x.. dy= 0.24.x=2x=2Ax=0.02Ar=0.02高等数学（上册）

例1 解 2, 0.02 . 求函数 y  x 3 当 x  x  时的微分 dy  (x )x 3  3 . 2  x x 0.02 2 2 0.02 d 2 3          x x x y x x x  0.24. 因为微分dy  f (x)dx  f (x)x

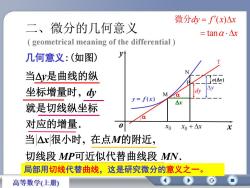
微分dy= f'(x)△x二、微分的几何意义= tanα:△x(geometrical meaning of thedifferential)yt几何意义：（如图）1N当△y是曲线的纵10(Ar)Aydy坐标增量时，dyMKa= f(x)Ar就是切线纵坐标Ja对应的增量oXo +△xxox当△x|很小时，在点M的附近切线段MP可近似代替曲线段MN局部用切线代替曲线，这是研究微分的意义之一。6高等数学（上册）

二、微分的几何意义 y  f ( x) 0x M N T dy y o(x) ） x y o  x 几何意义:(如图) . , 对应的增量 就是切线纵坐标 坐标增量时 当 是曲线的纵 dy y x  x 0 P . , , MP MN x M 切线段 可近似代替曲线段 当  很小时 在点 的附近 ( geometrical meaning of the differential ) ） ( ) tan dy f x x  x      微分 局部用切线代替曲线，这是研究微分的意义之一

三基本初等函数的微分公式与微分运算法则dy = f'(x)dx微分的计算公式：微分就是导数与的乘积求法：计算函数的导数，乘以自变量的微分1.基本初等函数的微分公式d(x")= μxu-ldxd(C)= 0d(sin x) = cosxdxd(cosx) = -sin xdxd(tan x) = sec* xdxd(cot x) = -csc2 xdxd(secx) = secxtanxdxd(cscx)=-cscxcotxdx(sinx)=cosx =dsinx=cosxdx高等数学（上册）

三基本初等函数的微分公式与微分运算法则 dy  f (x)dx 求法: 计算函数的导数, 乘以自变量的微分. 1.基本初等函数的微分公式 x x x x x x x x x x x x x x x x x x x x C x x x d(sec ) sec tan d d(csc ) csc cot d d(tan ) sec d d(cot ) csc d d(sin ) cos d d(cos ) sin d d( ) 0 d( ) d 2 2 1              