《高等数学》课程教学资源（课件讲稿）第三章_3.5.2

第三节导数的应用渐近线函数图形的描绘小结思考题高等数学（上册）

渐近线 第三节 导数的应用 小结 思考题 函数图形的描绘

一、渐近线(asymptotes)定义当曲线y=f(x)上的一动点P沿着曲线移向无穷点时,如果点P到某定直线L的距离趋向于零,那么直线L就称为曲线y=f(x)的一条渐近线(垂直于x轴的渐近线)1.铅直渐近线如果lim f(x)=0 或 lim_f(x)= 80x→xxx那么x=x,就是y= f(x)的一条铅直渐近线11如y=(=8lim(x + 2)(x - 3)x=-2 (x + 2)(x - 3)1=8lim铅直渐近线:x=-2,x=3x-3 (x + 2)(x -3)高等数学（上册）

定义 当曲线y  f (x)上的一动点P沿着曲线 1. 铅直渐近线 如果 移向无穷点时,如果点 P 到某定直线 L的距离 趋向于零,那么直线 L 就称为曲线 y  f (x)的 那么   x x0 x  x0就是y  f (x)的一条 一、渐近线(asymptotes) 铅直渐近线. lim f (x)   或 lim f (x)    x x0  一条渐近线. 如 , ( 2)( 3) 1    x x y 铅直渐近线:x  2, ( 2)( 3) 1 lim x2 x  x  ( 2)( 3) 1 lim x3 x  x  x  3.     (垂直于x轴的渐近线)

1例如y:(x + 2)(x - 3)V212-1.-2x = 3.有铅直渐近线两条：x=-2,高等数学（上册）

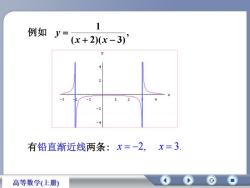
例如 , ( 2)( 3) 1    x x y 有铅直渐近线两条: x  2, x  3

（平行于x轴的渐近线）（horizontal2.水平渐近线asymptotes如果limf(x)=b 或lim f(x)=b (b为常数)x→+8x→那么=b就是=f(x)的一条水平渐近线如 y= arctanx,元lim arctanx =0.52x-→+-5510151015元-0.lim arctanx =2x→-80元元水平渐近线两条：22一高等数学（上册）

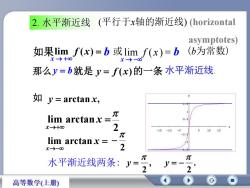
2. 水平渐近线 如果 如 y  arctan x, 水平渐近线两条: , 2  y    x x lim arctan   x x lim arctan 那么 . 2  y   lim f (x)  y  b就是 y  f (x)的一条 水平渐近线. x   x   b 或 b (b为常数) 2  2   (平行于x轴的渐近线) (horizontal asymptotes) lim f ( x ) 

3.斜渐近线(inclined asymptotes)如果lim [f(x)- (ax +b)] = 0X或 lim[f(x)-(ax+b)]=0(a,b为常数)X→-那么=ax+b就是=f(x)的一条斜渐近线下面求计算a,b的公式： lim ={f(x)-(ax+b)=0由上式和x为无穷大，有x→00Xf(x)f(x)bJima=0即 limx→±0x10xx斜渐近线求法：f(x)lima=l求出a后，将a代入可确定b,x→±xb = lim [f(x) -ax]高等那上ax+b就是曲线y=f(x）的一条斜渐近线

(inclined asymptotes) lim [ ( ) ( )] 0 lim [ ( ) ( )] 0 ( , ) ( ) . x x f x ax b f x a y x b a b ax b y f x              如果 或 为常数 那么 就是 的一条斜渐近线 斜渐近线求法: 那么 y  ax  b 就是曲线 y  f (x)的一条斜渐近线. 3. 斜渐近线 求出a后, b lim [ f (x) ax] x    x f x a x ( ) lim   将a代入可确定b, 下面求计算 a,b的公式 : 由上式和 [ ( ) ( )] 0 1 lim     f x ax b x x x为无穷大,     ] ( ) lim [ x b a x f x x    a x f x x ( ) lim 0 有 即

注f(x)如果b=limlf(x)-axllima=→±-→士00Xf(x)不存在;(1)limx-→±xf(x)a 存在,但 lim[f(x)一ax]不存在,(2) limx-→±ox→±0x可以断定=f(x)不存在斜渐近线。2(x - 2)(x + 3)例求f(x)=的渐近线。x-1解 定义域(-0,1)U(1,+),: lim f(x)= 00,x-→1x=1是曲线的铅直渐近线。lim f(x)=+0,lim f(x)=-o不是常数，极限不存在.故没有水平渐近线家高等数学（上册）

; ( ) (1) lim 不存在 x f x x , ( ) (2) lim a 存在 x f x x   可以断定 y  f ( x) 不存在斜渐近线. 例 . 1 2( 2)( 3) 求 ( ) 的渐近线     x x x f x 解 (,1)(1,). 注   lim ( ) 1 f x x  ,  x  1是曲线的铅直渐近线. 如果 但 lim [ f ( x) ax]不存在, x   b lim [ f (x) ax] x    , ( ) lim x f x a x  定义域 lim ( ) , lim ( ) x x f x f x      不是常数,极限不存在.故没有水平渐近线

2(x-2)(x+3）的渐近线。求 f(x):x-12f(x)b= lim[f(x)-ax]a=lim线limX-→±8士8x→0f(x)2(x - 2)(x + 3)=2=a又: limlimx(x -1)X-→00xX-→00lim[f(x) - ax] =lim[f(x) -2x]x>8x802(x - 2)(x + 3)-2xl= limlx-1x-→2(x - 2)(x + 3) - 2x(x -1)4=b= limx-1X-→00：y=2x+4是曲线的一条斜渐近线。C高等数学（上册）

   x f x x ( ) 又lim ( 1) 2( 2)( 3) lim     x x x x x  2 2 ] 1 2( 2)( 3) lim[ x x x x x       1 2( 2)( 3) 2 ( 1) lim        x x x x x x  4  y  2x  4 是曲线的一条斜渐近线 .      1 2( 2)( 3) lim x x x x 无水平渐近线    lim[ f (x) ax] x . 1 2( 2)( 3) 求 ( ) 的渐近线     x x x f x lim[ f (x) 2x] x   b lim [ f (x) ax] x    , ( ) lim x f x a x   a  b

2(x - 2)(x + 3)f(x)=的两条渐近线如图x-1Y10050y=2x+4xx4-4-22-50-100高等数学（上册）

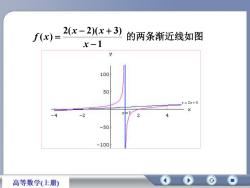
的两条渐近线如图 1 2( 2)( 3) ( )     x x x f x x 1 y  2x  4

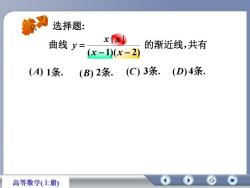
习选择题:x曲线 y=的渐近线，共有(x -1)(x - 2)(B)2条． (C) 3条。 (D)4条.(A) 1条.高等数学（上册）

曲线 的渐近线， ( 1)( 2) | |    x x x x y 共有 (B) (A) 选择题: 1条. 2条. (C) 3条. (D) 4条

二、函数图形的描绘如果函数f(x)的定义域上的某个小区间中（1）单调性已知；(2）凹凸性已知；（3）区间端点的位置已知或变化趋势已知；那么可以很容易地画出函数在这个区间内的图形高等数学（上册）

二、函数图形的描绘 如果函数 f (x) 的定义域上的某个小区间中 （1）单调性已知； （2）凹凸性已知； （3）区间端点的位置已知或变化趋势已知； 那么可以很容易地画出函数在这个区间内的图形．