《高等数学》课程教学资源（课件讲稿）第三章_3.3

第五节泰勒(Taylor)公式问题的提出一、、Pn和Rn的确定二、三、泰勒中值定理四、简单应用五、小结思考题高等数学（上册）

一 、问题的提出 二、Pn和Rn的确定 四、简单应用 五、小结 思考题 三、泰勒中值定理 第五节 泰勒(Taylor)公式

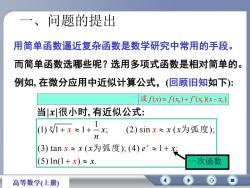
一、问题的提出用简单函数逼近复杂函数是数学研究中常用的手段。而简单函数选哪些呢？选用多项式函数是相对简单的。例如，在微分应用中近似计算公式，(回顾旧知如下)：或 f(x)= f(x)+ f'(x)(x-xo)当x很小时，有近似公式：(1) r/1+ x ~1+=x;(2) sin x ~ x(x为弧度):n(3) tan x~ x(x为弧度); (4)e*～ 1 +x一次函数(5) ln(1 + x) ~ x.高等数学（上册）

一、问题的提出 而简单函数选哪些呢？ 用简单函数逼近复杂函数是数学研究中常用的手段。 选用多项式函数是相对简单的。 例如, 在微分应用中近似计算公式，(回顾旧知如下): 1 (1) 1 1 ; (2) sin ( ); (3) tan ( ); (4) 1 ; (5) ln(1 ) . x n x x x x x n x x e x x x x          为弧度 为弧度 0 0 0 或 f (x)  f (x )  f (x )(x  x ). 一次函数

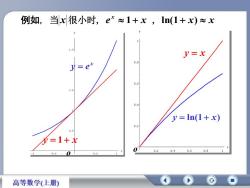
例如，当x很小时，e*～1+x ，In(1+x)～x42.5y=x0.800.61.50.4y = In(1 + x)0.20:5=1+x00.20.40.60.800.50.5高等数学（上册）

x y  e y  1 x o x y  e o y  x y  ln(1  x) 例如, 当 x 很小时, e x x  1 , ln(1 x)  x

不足：1、精确度不高；2、误差不能估计.寻找多项式函数P(x),使得f(x)~P(x)问题：误差 R(x)=f(x)-P(x),可估计设函数f(x)在含有x,的开区间(a,b)内具有直到(n+1)阶导数，P(x)为多项式函数P,(x)=a +a(x-x)+a,(x-x)+...+a,(x-x)误差R,(x)= f(x)-P,()如何确定P和R？高等数学（上册）

不足: 问题: 1、精确度不高； 2、误差不能估计. ●设函数 f (x)在含有 0 x 的开区间(a,b)内 具有直到(n  1) 阶导数, ●P( x)为多项式函数 n Pn (x) a a (x x ) a (x x ) an (x x ) 0 2  0  1  0  2  0   ●误差 R (x) f (x) P (x) n   n 如何确定 Pn 和 Rn ？ f (x)  P(x). 误差 R(x)  f (x)  P(x) ,可估计

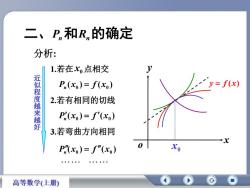
二、P,和R,的确定分析:1.若在x点相交近似程度越来越好y= f(x)P,(x)= f(x)2.若有相同的切线P'(x)= f'(x)3.若弯曲方向相同xP'(xo)= f"(xo)高等数学（上册）

二 、Pn和Rn的 确 定 x0 y  f (x) o x y 分析: ( ) ( ) 0 x0 P x f n  ( ) ( ) 0 x0 P x f n   ( ) ( ) 0 x0 P x f n     2.若有相同的切线 3.若弯曲方向相同 近似程度越来越好 1.若在 x0点相交

P(x)=a+a(x-x)+a(x-x)+.+a(x-x)假设: P(k)(x)= f(k)(x) k=1,2,,n 则a = f(x.),1.a, = f'(x,),2!a, = f"(x.)n!a, = f("(x.)得k(k = 0,1,2,..,n)酒k!代入P,(x)中得f"x.P(x) = f(xo)+ f'(xo)(x - xo)+2!xo)(x- x)"+n!高等数学（上册）

( ), 0 x0 a  f 代入P (x) n 中得 n n n x x n f x x x f x P x f x f x x x ( ) ! ( ) ( ) 2! ( ) ( ) ( ) ( )( ) 0 0 ( ) 2 0 0 0 0 0            得 ( ) ( 0,1,2, , ) ! 1 0 ( ) f x k n k a k k    1 ( ), 1 x0  a  f  2! ( ) 2 x0 a  f   , ! ( )0 ( ) n a f x n  n  P x f x k n k k n ( ) ( ) 1,2, , 0 ( ) 0 假设: ( )    则 n Pn (x) a a (x x ) a (x x ) an (x x ) 0 2  0  1  0  2  0  

三、泰勒(Taylor)中值定理如果函数f(x）在含有x.的某个开区间（ab内具有直到(n+1)阶的导数，则当x在（a.b)内时，f(x)可以表示为(x一x)的一个n次多项式与一个余项Rx)之和：f"(xo(x-x)f(x)= f(x)+ f(x(x -x)+2!(x-x)" + R,(x)n!(x-x)n+l，（在x与x,之间)其中R,(x)=(n+1)!拉格朗日余项带拉格朗日型余项的n阶泰勒Taylor公式

三、泰勒( Taylor )中值定理: 如果函数 f (x)在含有 0 x 的某个开区间(a,b) 内具有直到(n  1)阶的导数,则当x在(a,b)内 时, f (x)可以表示为( ) 0 x  x 的一个n次多项 式与一个余项R (x) n 之和: 0 2 0 0 0 0 ( ) 0 0 ( ) ( ) ( ) ( )( ) ( ) 2! ( ) ( ) ) ! ( n n n f x f x f x f x x x x x f x x x R x n           ( 1) 1 0 0 ( ) ( ) ( ) , ( . ( 1)! n n n f R x x x x x n        其中 在 与 之间) 拉格朗日余项 带拉格朗日型余项的n阶泰勒Taylor公式

（n+1）()(x -x)"+1(在x,与x之间)R,(x) =(n + 1):拉格朗日形式的余项若x E(a,b),I f(n+I)(x)< M, 则f(n+1) (2)Mn+1n+1R,(x):x-(n + 1):R,(x)及 lim=0x-x (x-xo)"即 R,(x)=o[(x-x)"].佩亚诺形式的余项(x2) +o[(x-x)"]: f(x)=r.k!k=0高等数学（上册）

拉格朗日形式的余项     1 0 1 0 ( 1) ( ) 1 ! ( ) 1 ! ( ) ( )          n n n n x x n M x x n f R x  ( ) [( ) ] ! ( ) ( ) 0 0 0 0 ( ) k n n k k x x o x x k f x  f x         ( ) ( ) 1 ! ( ) ( ) 0 1 0 ( 1) x x 在x 与x之间 n f R x n n n        佩亚诺形式的余项 0 ( ) ( ) lim 0 0    n n x x x x R x 及 ( ) [( ) ]. 0 n 即 Rn x  o x  x 若x(a,b), | f (n1) (x) | M , 则

在不需要余项精确表达式时，n阶泰勒Taylor公式可以写成：设函数f(x)在x处有0～n阶导数,则f"(xo)f(x) = f(x)+ f(x)(x-xo)(x-x)2!(n(xo+·+(x- x)" +o[(x- x)"]n!或f(k)(x)(x -x)* +o[(x-x)"k!k=0佩亚诺Peano型余项其中 R,(x)= o[(x-xo)")带佩亚诺Peano型余项的n阶泰勒Taylor公式

0 2 0 0 0 0 ( ) 0 0 0 ( ) ( ) ( ) ( )( ) ( ) 2! ( ) ( ) ! [( ) ] n n n f x f x f x f x x x x x f x x x o x x n            在不需要余项精确表达式时, n阶泰勒 Taylor 公式可以写成： 0 f (x) x 0  n ( ) 0 0 0 0 ( ) ( ) [ ! ( ) ] n k k n k f x x x o x x  k     或 带佩亚诺 Peano 型余项的n阶泰勒 Taylor 公式. 佩亚诺 Peano型余项 0 (x) [( ) ] n Rn 其中  o x  x

r(k)(x(sW4注意：f(x)=Xk!(n+1)!k=01.当n=0时，泰勒公式变成拉氏中值公式(在x,与x之间)f(x)= f(x)+ f'()(x-x)(0()M+2. 取x。 = 0, =→ f(x)=)k!(n+ 1)!在0与x之间,令=x(0<0<1)f(n+1) (x)th+1则余项R,(x) :(n + 1)!I麦克劳林（Maclaurin）公式高等数学（上册）

注意: 1. 当n  0时,泰勒公式变成拉氏中值公式 ( ) ( ) ( )( ) ( ) f x  f x0  f   x  x0 在x0与x之间 ( ) ( 1) 0 1 0 0 0 ( ) ( ) ( 1)! ( ) ( ) ( ) ! n k k k n n f x f x f x x n x x k           2.取x0  0,  在0与x之间,令  x (0    1) 则余项 1 ( 1) ( 1)! ( ) ( )     n n n x n f x R x  ( 0 ( 1) 1 ) ( ) ( ) ! 0 ( ) ( 1)! n k k n n k f f x x k f x n          麦克劳林( Maclaurin )公式