《高等数学》课程教学资源（课件讲稿）第三章_3.2

第二节洛必达法则0、x→a时的型未定式/00二、当x→8时的型未定式及当x→08型未定式或x→8时的三、0.80、8-80、0、1、8°型未定式四、小结思考题高等数学（上册）

四、小结 思考题 第二节 洛必达法则 一、x  a时的 0 0 型未定式 二、当x  时的 0 0 型未定式及当x  a 或x  时的   型未定式 三、0 、  、 0 0 、  1 、 0  型未定式

0一、x→a 时的型未定式解法：洛必达法则0（L'Hospital-Bernoullirule)）定义如果当x→α(或x→)时，两个函数f(x)与 F(x)都趋于零或都趋于无穷大，那么f(x)可能存在、也可能不存在．通极限limF(x)x-→a(x→00)08或型未定式常把这种极限称为08In sin ax8tanxlim例如,limx-0 In sin bx8x-→0x高等数学（上册）

一、 时的 型未定式解法 :洛必达法则 0 0 x  a 定义 例如, , tan lim 0 x x x , lnsin lnsin lim 0 bx ax x ) 0 0 ( ( )   ( L’Hospital-Bernoulli rule ) ( ) ( ) ( ) ( ) ( ) lim ( ) x a x x a x f x F x f x  F x  如果当  或   时，两个函数 与 都趋于零或都趋于无穷大，那么 极限 可能存在、也可能不存在．通 . 0 0 常把这种极限称为 或 型未定式  

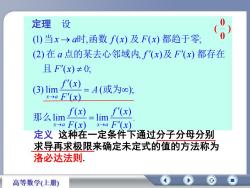
设定理(I)当x→α时,函数f(x)及 F(x)都趋于零(2)在a点的某去心邻域内,f(x)及 F(x) 都存在且 F'(x)±0;f'(x)A(或为∞);(3) limF'(xx-af(x)(x那么lim: limF(x)F(x)x->ax>a定义这种在一定条件下通过分子分母分别求导再求极限来确定未定式的值的方法称为洛必达法则高等数学（上册）

(1) , ( ) ( ) ; (2) , ( ) ( ) ( ) 0; ( ) (3) lim ( ); ( ) ( ) ( ) lim lim . ( ) ( ) x a x a x a x a f x F x a f x F x F x f x A F x f x f x F x F x                设 当 时 函数 及 都趋于零 在 点的某去心邻域内 及 都存在 且 或为 那么 定理 定义 这种在一定条件下通过分子分母分别 求导再求极限来确定未定式的值的方法称为 洛必达法则

0f'(x)如果仍属型，且 f'(x),F(x)满足0F'(x)使用洛必达法则，即定理的条件，可以继续f(x)f"(x)f'(x)linJinx-a F'(x)x-a F"(x)x-→a F(x)tanx例1求 limx-→0x(tan x)"sec-X解原式=lim:lim1(x)x-→0x-→0或利用等价无穷小代换更为简单。高等数学（上册）

定理的条件，可以继续 使用洛必达法则，即 如果 仍属 型，且 ( ), ( ) 满足 0 0 ( ) ( ) f x F x F x f x     . ( ) ( ) lim ( ) ( ) lim ( ) ( ) lim            F x f x F x f x F x f x x a x a x a 例1 解 . tan lim 0 x x x 求 ( ) (tan ) lim 0     x x x 原式 1 sec lim 2 0 x x   1. ) 0 0 ( 或利用等价无穷小代换更为简单

x3 -3x+2例2 求 limx-x-x+1-13x2-336x解?原式=limlimx=i3x2-2x-12x-1 6x - 26xlim注意：上式中的已不是未定式，不能x-1 6x - 2再对它应用洛必达法则，否则会导致错误结果在多次使用洛必达法则时，一定要注意验证是否满足条件高等数学（上册）

例2 解 . 1 3 2 lim 3 2 3 1       x x x x x x 求 3 2 1 3 3 lim 2 2 1      x x x x 原式 6 2 6 lim 1    x x x . 2 3  ) 0 0 ( 注意： 在多次使用洛必达法则时，一定要注意验证 是否满足条件．

0二、当x→8时的型未定式及当x→或0x→8时的=天型未定式8当x→8时的未定式以及x→a,或x→80时的未定式都有相应的洛必达法则，8高等数学（上册）

二、当 x  时的 0 0 型未定式及当 x  a或 x  时的   型未定式 , . , , 0 0 时的未定式 都有相应的洛必达法则 当 时的未定式 以及 或   x   x  a x  

8型的洛必达法则为：如x→a时的未定式8如果2e8(I) lim f(x) = lim F(x)= 00;x-→ax→a(2)在a 点的某去心邻域内,f'(x)及 F(x)都存在且 F(x)≠ 0;f(x)= A (或为);(3) limF(x)x-→af(x)(x那么limlimF(x)F'(x)x-→ax-→a高等数学（上册）

(1) lim ( ) lim ( ) ; (2) , ( ) ( ) ( ) 0; ( ) (3) lim ( ); ( ) ( ) ( ) lim lim . ( ) ( ) x a x a x a x a x a f x F x a f x F x F x f x A F x f x f x F x F x                    如果 在 点的某去心邻域内 及 都存在且 或为 那么

元arctanx2例3 求 lim1X→+0x122x1± x解 原式= limlim1x→+1+xx→+00高等数学（上册）

例3 解 . 1 arctan 2 lim x x x    求 2 2 1 1 1 lim x x x      原式 2 2 1 lim x x x     1. ) 0 0 (

In sin ax例4求 limx-→0 In sin bx81cosax:asin bx ·cosax ·a解sin ax原式=lim=lim1x→0x-→0 sinax ·cosbx·bcosbx·bsin bx等价无穷小代换bx 1.alim=x-→0 ax.1.b1.中高等数学（上册）

例4 解 . lnsin lnsin lim 0 bx ax x 求 0 0 1 cos sin cos sin lim lim 1 sin cos cos sin x x ax a ax bx ax a ax bx b bx b bx           原式 0 1 lim x 1 bx a  ax b      等价无穷小代换  1

tanx例5求 lim元tan3x8?x→23xsec'xcos"解 原式=limCos?~3sec*3x3元xx-222cos3x·(-sin3x).3cos 3x ·(-(-1))= limlim元3 x一元cos x ·(-1)2cos x ·(-sin x)Y221.3(-sin 3x) .31mlim3.元- sin x1元X2X-注：不可用等价无穷小代换，因这里不是x趋近于0家高等数学（上册）

例5 解 . tan3 tan lim 2 x x x   求 x x x 3sec 3 sec lim 2 2 2   原式  x x x 2 2 2 cos cos 3 lim 3 1    2 1 2cos3 ( sin 3 ) 3 lim 3 x 2cos ( sin ) x x x x         2 ( sin 3 ) 3 lim x sin x x        2 1 3 lim x 1      3. ( )   2 cos3 ( ( 1)) lim x cos ( 1) x x        