《线性代数》课程教学资源（课件讲稿，B）第二章行列式_2-1n阶行列式的定义

第二章s1n阶行列式的定义一、二阶行列式的定义二、三阶行列式的定义三、n阶行列式的定义加油！

§1 n阶行列式的定义 第二章 一、二阶行列式的定义 二、三阶行列式的定义 三、n阶行列式的定义

二元一次线性方程组求解(1)aiiXi + a12xX2 = br,(2)a21Xi + a22X2 = b2.用高斯消元法求其解：_ (1) ×a22a1a22X + 12a22x2 = b,a222←← (2)×ali2a21a12Xi +a22a12x2 =b,a12?(aa22 a12a21) Xj = b,a22 -b,a12加油！

       . , 21 1 22 2 2 11 1 12 2 1 a x a x b a x a x b 1 2 22 (1)  a 12 ) (2)  a 11 22 12 21 1 1 22 2 12 （a a a a x b a b a    ） 用高斯消元法求其解： 21 12 1 22 12 2 2 12 a a x a a x b a   11 22 1 12 22 2 1 22 a a x a a x b a   二元一次线性方程组求解

(1)a11Xi + a12X2 = b1(2)a21Xi +a22Xz =b2.a2ialx +a22aiix2 = b,a1 (2)×al1← (1)×a21a,a21x; + ai2a21X, = b,a21(aa22 aiza21) X, = b,a -b,a21加油！

       . , 21 1 22 2 2 11 1 12 2 1 a x a x b a x a x b 1 2 11 22 12 21 2 2 11 1 21 （a a a a x b a b a    ） 21 11 1 22 11 2 2 11 a a x a a x b a   11 (2)  a 21 ) (1)  a 11 21 1 12 21 2 1 21 a a x a a x b a  

(aia22 -a12a21) X, = b,a22 -b,a12ax +aix = b,a21xj +a22x2 =b,(aa22 -ai2a21) X2 = b,al1 -ba21(a11α22 -12α21 ± 0)Ab,a22 -b,ai2xaia22 -a2α211222b,au -b,a21aα22 -ai2α21加油！

11 22 12 21 1 1 22 2 12 （a a a a x b a b a    ） 11 22 12 21 2 2 11 1 21 （a a a a x b a b a    ） 1 22 2 12 1 11 22 12 21 b a b a x a a a a    2 11 1 21 2 11 22 12 21 b a b a x a a a a    11 1 12 2 1 21 1 22 2 2 , . a x a x b a x a x b        11 12 21 22 a a A a a        1 12 1 2 22 b a A b a        11 1 2 21 2 a b A a b       

二阶行列式定义由四个数排成二行二列（横排称行、竖排称列的数表aay2a21a22数[a1a22 - a12a2称为数表所确定的二阶行列式，记为aa12a21122加油！

由四个数排成二行二列（横排称行、竖排称列） 的数表 数 a a a a 11 22 12 21  称为数表所确定的 二阶行列式, 记为 11 12 21 22 a a a a 二阶行列式定义 11 12 21 22 a a a a

三阶行列式的引出aiiar2ar3aiix+ai2x+ai3xg=bA=a21Xi+a22X2 +a23Xg =b2a22a21a23a31 +a32X +a33xg =b3a31a32a33当detA+0(A|+0)时，三元线性方程组的解为det A,det A,det A,A,AAX2X3X,[AAAdet Adet Adet A66barlaila13ar2a2a3b26b,a21a22a22a23a232a21byLba32a32a31a33a31a33加油！

  1 2 3 1 2 3 1 2 3 det 0 det det det , , det det det A A A A A A A A x x x A A A A A A         当 0 时，三元线性方程组的解为： 11 12 13 21 22 23 31 32 33 a a a A a a a a a a            1 12 13 1 2 22 23 3 32 33 b a a A b a a b a a                          31 1 32 2 33 3 3 21 1 22 2 23 3 2 11 1 12 2 13 3 1 a x a x a x b a x a x a x b a x a x a x b 11 1 13 2 21 2 23 31 3 33 a b a A a b a a b a            11 12 1 3 21 22 2 31 32 3 a a b A a a b a a b            三阶行列式的引出

推广ax +a2x +...+anx, =bAdet A,a21xi +a22X2 +...+a2nxn = b2xAdet Aanx +an2X2 +...+amx,=b2det AA.nnaia12ainXAdet Aa21azna,当 det A[4+0 时,.anianna,b,6anOb.baazna21det:,det A.b.b.amnanlaa加油！

11 12 1 21 22 2 1 1 det 0 n n n n nn a a a a a a A A a a a 当    时, 推广 1 1 1 det det det det n n n A A x A A A A x A A              1 12 1 11 12 1 2 22 21 22 2 2 1 1 1 1 1 det , , det n n n n n n nn n n n b a a a a b b a a a b a A A A A b a a a a b     11 1 12 2 1 1 21 1 22 2 2 2 1 1 2 2 n n n n n n nn n n a x a x a x b a x a x a x b a x a x a x b                   

三阶行列式定义设有9个数排成3行3列的数表a1a13a2(5)121a22a23a33(3)a32记a11a13a12(6)=ai12233 +12a23a31 +a132132a21a22(23a1a23a32 -a2a21a33 -a13a22a31,a31a32a33(6)式称为数表（5）所确定的三阶行列式加油！

三阶行列式定义 31 32 33 21 22 23 11 12 13 (5) 9 3 3 a a a a a a a a a 设 有 个数排成 行 列的数表 记 11 23 32 12 21 33 13 22 31, 11 22 33 12 23 31 13 21 32 (6) a a a a a a a a a a a a a a a a a a       31 32 33 21 22 23 11 12 13 a a a a a a a a a （6）式称为数表（5）所确定的三阶行列式

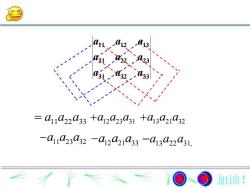
23asth33= a1122α33 +a12α23α31 +a13a21α32-a23α32 -a2α23 -α22α31,加油！

31 32 33 21 22 23 11 12 13 a a a a a a a a a 13 21 32 a a a 12 21 33 a a a 12 23 31 a a a 11 22 33  a a a 11 23 32 a a a 13 22 31, a a a

n阶行列式定义ain(lai,j-1a,j+1ana;-1,j-1a;-1,j+1ai-1,ndet A =ai-1,11a;+1,j-1a;+1,j+1a;+1,nli+1,1aanlnnannanan,j-1an,j+1-------余子式n = 1, det A= aiiA, =(-1)" Mj----代数余子式n ≥ 2, det A = auA +a2A2 +...+ainA加油！

11 1, 1 1, 1 1 1,1 1, 1 1, 1 1, 1,1 1, 1 1, 1 1, 1 , 1 , 1 j j n i i j i j i n ij i i j i j i n n n j n j nn a a a a a a a a M a a a a a a a a                                      11 1 1 det n n nn a a A a a  n 阶行列式定义 -余子式 -代数余子式 11 11 11 12 12 1 1 1, det n 2, det n n n A a A a A a A a A         1 i j A M ij ij   