《高等数学》课程教学资源（知识拓展，数学竞赛8讲）第02讲 浅谈如何探索竞赛题的求解思路

第2讲浅谈如何探索竞赛题的求解思路以微分方程为例李海玲山东理工大学

第2讲 浅谈如何探索 竞赛题的求解思路 ——以微分方程为例 山东理工大学      李海玲

如何解题求解微分方程的一般思路与方法微分方程相关竞赛题分析数学竞赛全国大学生数学竞赛（初赛非全国大学生数学数学类)竞赛棋整解新百更薪244M用E订间视2009年第1届第1题（1）视量2009年第1届第1题（2）2009年第1届第二题

l 如何解题 l 求解微分方程的一般思路与方法 l 微分方程相关竞赛题分析

如何解题Horo&ohc怎样解题HowtoSolveIt理解题目解怎样题拟定方案数学思维的新方法执行方案E畅销七十年的解题经典检验反思激发无数人的聪明才智

一、如何解题 理解题目 拟定方案 执行方案 检验反思

一、如何解题第一步审题(理解题目)审题，复述问题、理解问题。标记，写出描述问题的关键性的字词与数学表达式，包括条件中的，也包括结论中的，并且明确条件与结论。第二，问题归类（拟定方案）中心思想：陌生问题熟悉化。这个步骤是探索大类问题解决思路的关键！改写条件、结论中的表达式为可能的各描述形式，转换、变形问题描述，对比已有知识结构中的问题类型，将问题题型小类归类为熟悉的问题！

一、如何解题 第一步 审题 (理解题目) 审题，复述问题、理解问题。标记，写出描述问题的关键性的字词 与数学表达式，包括条件中的，也包括结论中的，并且明确条件与 结论。 中心思想：陌生问题熟悉化。这个步骤是探索 问题解决思路的关键！改写条件、结论中的表 达式为可能的各描述形式，转换、变形问题描 述，对比已有知识结构中的问题类型，将问题 归类为熟悉的问题！ 第二，问题归类(拟定方案) 大类 题型 小类

一、如何解题第三思路探索（执行方案）可能题型各种可能的求解思路与方法，逐一探索；重新归类，拆分逐步解决。探索、完成求解验证的过程，其实就是一个根据目标，不断改写条件、结论表达式，构造相应求解方法的条件和需要的表达式的过程！第四检验反思数学竞赛全国大学生数学竞赛（初赛非全国大学生数学数学类）真掌握练习不在多而在精，多理解、鹿赛真隆解所包更薪24mB商股S订街触类旁通能延伸、会拓广，举一反三、投明2009年第1届第1题（1）2009年第1届第1题（2）授解2009年第1届第二题

一、如何解题 可能题型各种可能的求解思路与方法，逐一探索；重新归类，拆分 逐步解决。探索、完成求解验证的过程，其实就是一个根据目标， 不断改写条件、结论表达式，构造相应求解方法的条件和需要的表 达式的过程！ 第三 思路探索(执行方案) 第四 检验反思 练习不在多而在精，多理解、真掌握 能延伸、会拓广，举一反三、触类旁通

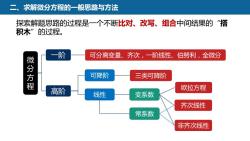
二、求解微分方程的一般思路与方法改写、探索解题思路的过程是一个不断比对、组合中间结果的“搭积木”的过程一阶可分离变量、齐次，一阶线性、伯努利，全微分微分方程可降阶三类可降阶欧拉方程高阶线性变系数齐次线性常系数非齐次线性

二、求解微分方程的一般思路与方法 探索解题思路的过程是一个不断比对、改写、组合中间结果的“搭 积木”的过程。 微 分 方 程 一阶 高阶 可分离变量、齐次，一阶线性、伯努利，全微分 可降阶 线性 三类可降阶 变系数 常系数 齐次线性 非齐次线性 欧拉方程

求解微分方程的一般思路与方法M (x)dx = N ()dy P 0 M (x)dx = 0 N (v)dy可分离变量微分方程dydudy=f(x)= j齐次微分方程uu+xexodxdxd.rye+P(W=Q()一阶线性微分方程0o0(x)e 0 P(c)dxy=eoP(x)dxadx +P0+P(=Q("(n0,1)伯努利方程du= (l- n)" dyu=I-nDdrdP(x,y)Q(x,)Pdx+Q(xdy=0全微分方程93qx1Q(xv)d=C或o"Q(xoV)dv+P(u,y)du=CP(uo)du+10D.0FO0YO

二、求解微分方程的一般思路与方法 可分离变量微分方程 齐次微分方程 一阶线性微分方程 伯努利方程 全微分方程

求解微分方程的一般思路与方法Mdx=NdyPOM()dx=ON()d)可分离变量微分方程Odudydyy= f (x,y)=uD齐次微分方程u+xExdxdxdxxye+P(W=Q()一阶线性微分方程0=eoP(r)dxao0(r/e0 P()dxdx+P0+P(=Q("(n0,1)伯努利方程du= (l- n)" dyu=I-nDdrdP(x,y)Q(x,)Pdx+Q(xdy=0全微分方程93qx1Q(xv)d=C或o"Q(xoV)dv+P(u,y)du=CP(uo)du+10D.0OVO

二、求解微分方程的一般思路与方法 可分离变量微分方程 齐次微分方程 一阶线性微分方程 伯努利方程 全微分方程

二、求解微分方程的一般思路与方法Mdx=NdyPOM()dx=ON(d)可分离变量微分方程dydudy1f(x)齐次微分方程Suu+xexodxdxd.rye+ P(x)y = Q(x)一阶线性微分方程0P y=e oP(x)dxgo0(re oPa)dxdx +福-0+P(x=Q("(n0,1)伯努利方程du= (l- n)n dyu=I-nddrP(x,y)Q(x,)P(rdx+Q(x)dy=0,全微分方程93qxXQ(xv)d=C或o"Q(xoV)dv+P(u,y)du=CP(u,yo)du+0D.0FO/YO

二、求解微分方程的一般思路与方法 可分离变量微分方程 齐次微分方程 一阶线性微分方程 伯努利方程 全微分方程

二、求解微分方程的一般思路与方法Mdx=NdyPOM()dx=ON(d)可分离变量微分方程Pdydudy1f(x)=齐次微分方程uu+xExOdxdxdrye+P(W=Q()一阶线性微分方程0o0(x)e 0 P(c)dxy=eoP(r)dxadx +D0e+ P(x)y = Q(x)y" (n 1 0, 1)伯努利方程du(- n)"dyyl-nsM二dxdxP(x,y)Q(x,)P(rdx+Q(x)dy=0全微分方程qyqx1Q(xv)d=C或o"Q(xoV)dv+P(u,y)du=CP(uJo)du+0D.0FO0YO

二、求解微分方程的一般思路与方法 可分离变量微分方程 齐次微分方程 一阶线性微分方程 伯努利方程 全微分方程