《高等数学》课程教学资源（知识拓展，数学竞赛8讲）第06讲 多元函数微分法及其应用

练习题判断下列二元函数当（α,y）一→（0,0)时二重极限与累次极限的存在性，由此可以得出二重极限存在性与两个累次极限存在性之间有什么样的关系？acyC-(1) f(α,y) =(2)Ta+y+yT1(3) f(α,y) =(α +y) sinsinay

练习参考解答-y?22ay(1) f(a,y) =(2) f(α,y)a?+y?a?+y?1lim f(x,y)lim lim f(x,y),lim lim f(x,y)(3) f(α, y) = (α + y)sin=sinx@X0yRyoxeXoXRXoyyyByOlim lim f(x,y)= lim lim f(x,y)= 0()lim f(x,y)= lim cosq sinqX@OPR0JROxROx@0TROJROlim lim f(x,y)= 1, lim lim f(x,y) = - 1(2)lim f(x,y)= limcos? g - sin?S2XROyROJROxRx@0r?0*PRO10e1111lim lim&x sinsin(3)o%y sin-sin(x+y)sin-sinRy@OxROJ1JxxyQ如果它们都存在，则三者相等仅知其中一个存在，推不出其它二者存在

练习参考解答 Ø 如果它们都存在，则三者相等 Ø 仅知其中一个存在，推不出其它二者存在

第6讲多元函数微分法及其应用李海玲山东理工大学

第6讲 多元函数微分法及其应用 山东理工大学 李海玲

一、几个基本概念及相互关系与计算多元函数偏导数的计算三、多元函数的几何应用四、多元函数的极值与最值

l 一、几个基本概念及相互关系与计算 l 二、多元函数偏导数的计算 l 三、多元函数的几何应用 l 四、多元函数的极值与最值

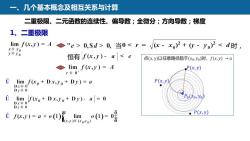
一、几个基本概念及相互关系与计算二重极限、二元函数的连续性、偏导数；全微分；方向导数；梯度1、二重极限lim f(x,y) = A"e> 0,$d> 0, 当0<r=V(x - xo)2 + (y - o)2 < d时 ,x?xoy?yo恒有f(x,j)- a< e点(x,y)以任意路径趋于(xo,yo)时，f(x,y）→alim f(x,y) = AP(x,y)rRO0P(x,y)limf(x+Dx,Jo+Dy)=aDXRODVROPo(to,yo)0lim,f(xo + Dx,yo+ Dy)-a= 0DXRODyROP(x,y)0 f(x,y)= a + o()lim0(1)=E(x)R(roVo)

一、几个基本概念及相互关系与计算 当 时， 恒有 1、二重极限 二重极限、二元函数的连续性、偏导数；全微分；方向导数；梯度

一、几个基本概念及相互关系与计算f(x,y)当(x,y) →(xo,yo)时的极限： limf(x,y) 9 ay-→yo[注) (x,y) → (xo,yo) = (x, y) → (0, 0):x-xo=ulimf(x,y) =limf(x,y) 令x-xoy-yo=Vy-yoy-yo→o= limf(u + xo, v + yo) = limg(u, v) = limg(x,y)1-V-→0-0y~0特殊路径法：当点(x,V)以不同方式趋于（00)时函数g（x，y）趋于不同值或有的极限不存在，则可以断定函数当(x,y）→(0,0)时极限不存在

一、几个基本概念及相互关系与计算

一、几个基本概念及相互关系与计算判断二元函数极限不存在的方法令x=pcos,y=psine，转换为单变量的极限问题极坐标法limf(x,y）=limf(pcoso,psinの）可以取任意值！-→y-0极限不存在极限为的表达式简化的极限式分母为e,的表达式r2cosqsinqlimlimr@ot ,*cos°g+ sin'q r = sin"q(@@ 0t,a >0)xB0JROcos' qsin2u.limsin4a-2q cosq + 1q@otr=sin"q

一、几个基本概念及相互关系与计算 判断二元函数极限不存在的方法 l 极坐标法 转换为单变量的极限问题 l 极限不存在

一、几个基本概念及相互关系与计算1-xy例求极限m0x2+2令x=pcoso,y=psing,y→11-xy1 - x(y+ 1)pcoso(psino + 1) +1lim=1.limlimx-0 x2 + y2x=0 x2 + (y + 1)22psin +p2 + 1p-0y-→1y-0点为(0,1)点为函数f(x,)=定义区域内的连续点:x2+v1-0.11-xylim x2 + y2= 1.02 + 12y→1

一、几个基本概念及相互关系与计算 例 求极限 = 1

一、几个基本概念及相互关系与计算2、二元函数连续性的判定如果函数在(xo,yo)某一邻域内有定义，并且有,limf(x,y）=f(xo,yo）y-yo则称函数f(x,y)在(xo,yo)处连续函数f(x,y)在(xo,yo)处连续：极限不仅存在而且等于f(xo,yo）多元初等函数在定义区域内是连续函数

一、几个基本概念及相互关系与计算 2、二元函数连续性的判定 并且有 多元初等函数在定义区域内是连续函数

一、几个基本概念及相互关系与计算3、二元函数偏导数与偏导函数的连续性分段二元函数在分段点、抽象函数偏导数存在性的讨论和偏导数的计算：f(x + 4x,y) - f(x,y)= fx(x, y)fl(x, y) =lim4x4x-→0f(x,y + 4y) -f(x,y)lim= ff(x,y)fy(x,y) =4y4y→0初等函数的偏导数仍然是初等函数，所以在定义区域内偏导函数仍然是连续函数?,(x,y)1 (0, 0),=0.(x,y)= (0, 0)

一、几个基本概念及相互关系与计算 3、二元函数偏导数与偏导函数的连续性 分段二元函数在分段点、抽象函数偏导数存在性的讨论和偏导数的计算： 初等函数的偏导数仍然是初等函数，所以在定义区域内偏导函数仍然是连续函数