《高等数学》课程教学资源（课件讲稿）第3章 第2讲 洛必达法则

高等数学（上册）第3章微分中值定理与导数的应用第2讲洛必达法则人民邮电出版社POSIS&TELECOMPRESS

高等数学（上册） 第2讲 洛必达法则 第3章 微分中值定理与导数的应用

RS人邮教育本讲内容w.nyjiaoyu.co0福01型未定式和型未定式0802其他类型的未定式0.8, 0, 8-8, 18,800

01 02 其他类型的未定式 “ ”型未定式和“ ”型未定式 0 0   本 讲 内 容 0, , 0 0 , 1 ,  0

001型未定式型未定式和COAORA人邮教育08定理3.4洛必达法则1设f(x)、g(x)在xo的某去心邻域内有定义，若(1) lim f(x)=0, lim g(x)=0 ;X-→Xo(2）f(x）)、g(x)在xo的某去心邻域内可导，且gx)±0;f'(x)lim(3)存在（或无穷大），g(x)x->x0f(x)f(x)limlim则g(x)g(x)x-xo-→Xo

01 “ ”型未定式和“ ”型未定式 0 0   定理 3.4 洛必达法则� 设 f (x) 、g(x) 在 x0 的某去心邻域内有定义，若 0 lim ( ) 0 x x f x  （  1） ，x l  im x0 g(x)  0； （2）f (x) 、g(x) 在x0的某去心邻域内可导，且g(x)  0； 0 ( ) lim ( ) x x f x  g x   （3） 存在（或无穷大）， 0 0 . ( ) ( ) lim lim ( ) ( ) x x x x f x f x  g x  g x    则 3

0e01型未定式型未定式和COAORA人邮教育08洛必达法则ⅡI定理3.5设f(x）、g(x)在xo的某去心邻域内有定义，若(1) lim f(x)=00, lim g(x)=00;X(2）f(x）、g(x）在x的某去心邻域内可导，且g(x)±0;f'(x)lim(3)存在（或无穷大），g(x)X-→Xof(x)f(x)limlim则X-Xox>xo g'(x)g(x)

定理 3.5 洛必达法则Ⅱ 设 f (x) 、g(x) 在 x0 的某去心邻域内有定义，若 0 lim ( ) x x f x  （1）   ，x l  im x0 g(x)   ； （2）f (x) 、g(x) 在x0的某去心邻域内可导，且g(x)  0； 0 ( ) lim ( ) x x f x  g x   （3） 存在（或无穷大）， 0 0 . ( ) ( ) lim lim ( ) ( ) x x x x f x f x  g x  g x    则 01 “ ”型未定式和“ ”型未定式 0 0   4

0e01型未定式型未定式和0000RA人邮教育08sinax求极限 lim例1(a,b为常数，且b±0）x-→0 sinbx0,该极限为型不定式，由洛必达法则，得o解000sinaxaacosaxlimlimbbcosbxx-0 sin bxx->0

例 1 5 0 0 解 该极限为“ ”型不定式，由洛必达法则，得 . a b  5 01 “ ”型未定式和“ ”型未定式 0 0   0 sin lim x sin ax  bx 求极限 （a, b 为常数，且b  0）. 0 0 0 0 sin cos lim lim x sin x cos ax a ax  bx  b bx 

0e01型未定式型未定式和CO0人邮教育RA08x-sinx求极限lim例）2r3-→00,解该极限为O型不定式，由洛必达法则，得0001-cosxsinxX-limlimx33x2x->0x->000sinx=lim6xx-→>016

例 2 6 0 0 解 该极限为“ ”型不定式，由洛必达法则，得 . 1 6  6 01 “ ”型未定式和“ ”型未定式 0 0   3 0 . sin lim x x x  x 求极限 3 2 0 0 0 0 sin 1 cos lim lim x x 3 x x x  x  x    0 0 0 sin lim x 6 x  x 

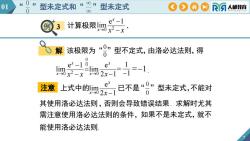
0401型未定式型未定式和CORA人邮教育08ex-1计算极限lim例3x-0 x2-xO,,该极限为型不定式，由洛必达法则，得解D001erCer-1-1limlim-1X-0 x2-x2x-1x0er0,注意已不是型未定式，不能对上式中的lim0x-02x-1其使用洛必达法则，否则会导致错误结果：求解时尤其需注意使用洛必达法则的条件，如果不是未定式，就不能使用洛必达法则

例 3 7 2 0 e 1 lim x x x x   计算极限 ． 0 0 该极限为“ ”型不定式，由洛必达法则，得 0 0 2 0 0 e 1 e lim lim 2 1 x x x x x x x     0 不是 e lim 2 1 x x x  0 0 上式中的 已 “ ”型未定式，不能对 其使用洛必达法则，否则会导致错误结果. 求解时尤其 需注意使用洛必达法则的条件，如果不是未定式， 能使用洛必达法则. 注意 就不 解 1 1   =1. 7 01 “ ”型未定式和“ ”型未定式 0 0  

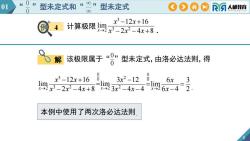
0e01型未定式型未定式和0000RA人邮教育08x3 -12x+16例计算极限limN-2x3-2x2-4x+80,该极限属于型未定式，由洛必达法则，得o解000003x3 -12x+163x2-126x-limlimlim2.x-2x3-2x2_4x+83x2_4x-46x-4x>2x-2本例中使用了两次洛必达法则

8 3 3 2 2 12 16 lim x 2 4 8 x x  x x x      计算极限 ． 0 0 该极限属于“ ”型未定式，由洛必达法则，得 0 3 2 0 3 2 2 2 2 12 16 3 12 lim lim x 2 4 8 x 3 4 4 x x x  x x x  x x          本例中使用了两次洛必达法则. 例 4 8 解 . 0 0 2 6 3 lim x 6 4 2 x  x    01 “ ”型未定式和“ ”型未定式 0 0  

001型未定式型未定式和00A0RA人邮教育08tanx-x例计算极限lim5xsinx.x-0"0,,这是型未定式，先对分母中的乘积因子解O0sinx利用等价无穷小x(x→0)进行代换，再由洛必达法则，得010Ssec2 x-1tanx-xtanx-xlim=lim=limX3x2X-40x?sinxX->0x-0tan? x11tanx>2Lim=lim3.3x23x→0x-0x

9 2 3 0 0 tan tan lim lim x sin x x x x x  x x  x    2 0 tan lim x sin x x  x x 计算极限 ． 0 0 这是“ ”型未定式，先对分母中的乘积因子 sin x利用等价无穷小 x (x  0)进行代换， 再由洛必达法则，得 2 0 1 tan lim( ) 3 x x  x  例 5 9 解 0 2 0 2 0 sec 1 lim x 3 x  x   2 2 0 tan lim x 3 x  x  . 1 3  01 “ ”型未定式和“ ”型未定式 0 0  

08e5L01型未定式和型未定式COAORA人邮教育080Inx例计算极限lim(nEN+)6x-→+001O解100Inx00门xlimlimlim=0nxn-1x-→+00x->+00x→+00 nx

10 ln lim ( ). n x x n N x   例 6 计算极限  解 01 “ ”型未定式和“ ”型未定式 0 0   1 1 ln 1 lim lim lim 0. n n n x x x x x x nx nx         