《高等数学》课程教学资源（课件讲稿）第2章 第4讲 函数的微分

高等数学（上册）第2章导数与微分第4节函数的微分人民邮电出版社POSTS&TELECOMPRESS

高等数学（上册） 第4节 函数的微分 第2章 导数与微分

R人邮教育本讲内容w.ryjinoyu.c01微分的概念02微分的几何意义03微分的计算04微分的应用

01 微分的概念 02 微分的几何意义 03 微分的计算 04 微分的应用 本 讲 内 容

一、微分的概念引例：一块正方形金属薄片受温度变化的影响，其边长由xo变到xo口□x，问此薄片面积改变了多少？设薄片边长为x，面积为A，则Ax2，当x在xo取得增量x时，面积的增量为XoxXA (x。x)?x22xox (x)LxXoAxoXox口0时为关于△x 的高阶无穷小线性函数故A2xx称为函数在Xo的微分HIGH EDUCATION PRESS

一、微分的概念 引例: 一块正方形金属薄片受温度变化的影响, 问此薄片面积改变了多少? 设薄片边长为 x , 面积为 A , 则 面积的增量为 关于△x 的 线性函数 高阶无穷小 时为 故 称为函数在 的微分 当 x 在 取 得增量 时, 边长由 变到 其

01微分的概念OOOORA人邮教育定义2.4设函数=f(x)在xo的某邻域U(xo)内有定义,x+DxiU(xo)，若函数增量Dy=f(x。+Dx）-f(xo）可表示为(2. 4)Dy = ADx + o(Dx)其中A是不依赖于Dx的常数，而o(Dx)是比Dx高阶的无穷小，那么称函数y=f(x）在点xo是可微的.而ADx叫做函数f(x)在点xo相应于自变量增量Dx的微分，记作dylx=xo或df(x)x=xo"即dy =xo =ADx

定义2. 4 4 设函数 在 的某邻域 内有定义， ， 若函数增量 可表示为 (2. 4) 其中 A 是不依赖于 的常数，而 那么称函数 在点 是可微的. 是比 高阶的无穷小， 而 叫做函数 在 01 微分的概念 点 相应于自变量增量 的微分，记作 dy|x=x0 或 d f (x)| x=x0， 即

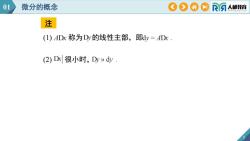
01微分的概念COARA人邮教育注(1)ADx称为Dy的线性主部，即dy=ADx(2) Dx很小时，Dy》dy

注 5 (2) 很小时， . 01 微分的概念 (1) 称为 的线性主部，即

01微分的概念OOOORA人邮教育定理2.6函数y=f(x)在xo处可微Uf(x)在xo处可导，且dy=fdxo)Dx.证：“必要性”已知=f(x)在点x可微，Dy= f(x +Dx)- f(x) = ADx +o(DxDyo(Dx)= lim(A+lim=ADrRoDxDxDrRO故 =f(x)在点xo的可导，且fdx)=A

6 函数 在 处可微 在 处可导，且 定理2.6 01 微分的概念 证: “必要性” 已知 在点 可微 , 故 在点 的可导, 且

01微分的概念OOOOR人邮教育定理2.6函数y=f(x)在xo处可微Uf(x)在xo处可导，且dy=fdxo)Dx.“充分性”证：Dy=fdxo)lim已知y=f(x)在点x。可导，DrRODXDy=fdxo)+a(lima =0)DxDr?0故 Dy= fdxo)Dx+a Dx = fdxo)Dx+o(Dx)即 dyr = f dxo)Dx

7 函数 在 处可微 在 处可导，且 定理2.6 01 微分的概念 证: 已知 在点 可导 , 即 “充分性

01微分的概念COAOR人邮教育注：记作dy=fdx)Dx函数在点x。的微分，1.规定dx=Dx，则dy=fdxo)dx2.函数在任意点x的微分，记作dy=fdx)Dx=fdx)dx

8 函数在点 的微分， 记作 1.规定 ，则 2.函数在任意点x的微分， 注： 记作 01 微分的概念

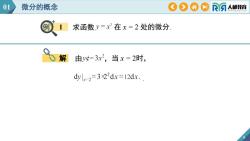
01微分的概念COA0R人邮教育例求函数V=x在x=2处的微分解由y=3x2，当x=2时,Ody lx=2=3×22dx =12dx

9 . 解 例 1 由 ，当 x = 2时， 求函数 01 微分的概念 在 x = 2 处的微分

01微分的概念OOAO人邮教育例2已知函数=x2，求：dy= fdx)dx(1)函数的微分;dylx-= fdx)Ax = fdxo)dx(2)函数在x=1处的微分;(3)函数在x=1处，当△x=0.02时的微分(1) dy =(x2)dx = 2xdx ;心解(2) dy |x=I= 2x x= dx = 2dx ;(3)dy=2' 0.02=0.04

10 解 例 2 01 微分的概念 已知函数 求： (1) 函数的微分； (2) 函数在 x = 1 处的微分； (3) 函数在 x = 1 处，当Δx = 0.02 时的微分. (1) (2) (3)