《线性代数》课程教学资源（章节讲稿，C）1-3 逆矩阵

逆矩阵1-3aα,=αα=l引入：对于任一实数 α1 0，则存在倒数满足对于任—n阶方阵A及单位矩阵IAI=IA=A，是否存在矩阵得AB=BA=I ?例如2 32 0a 32 Gel20acl62.FPcee.12322-alael:O.:0.00000!2o00a20:0.1'a22o.o.:0010111000→=1·1--30000-390000ce3630e

1-3 逆矩阵 引入：对于任一实数 ，则存在倒数 ， 满足 对于任一 n 阶方阵 A 及单位矩阵 I ， ，是否存在矩阵 B ，使 得 例如

定义1设 A为n阶方阵，若存在n阶方阵 B，使得=BA=I，则称A是可逆矩阵，简称矩阵A可逆，并称B是A的逆矩阵定理1设A是可逆矩阵，则其逆矩阵是唯一的。（反证法证明）若设B和C是A的可逆矩阵，则有AB = BA= E, AC =CA=E,可得 B=EB=(CA)B=C(AB)=CE=C所以A的逆矩阵是唯一的,记作A-1B=C=A

定义1 设 A为 n 阶方阵，若存在 n 阶方阵 B，使得 ，则称 A 是可逆 矩阵，简称矩阵 A 可逆，并称 B 是 A 的逆矩阵。 定理1 设 A 是可逆矩阵，则其逆矩阵是唯一的。 （反证法证明） 若设B和C是A的可逆矩阵，则有 可得 所以A的逆矩阵是唯一的,记作A -1

注（1）由定义可知，若B是A的逆矩阵，则A也是B的逆矩阵。（2）设矩阵A可逆，则存在唯一的逆矩阵，记为4-1A且=AA=I（3）矩阵A可逆一存在矩阵AB,-使得（4）单位矩阵I可逆，且I1=I（5）对角矩阵ad:0..且a1C:O.d,c-L=Ssdd, 1 0(i=1,2,L ,n)XC01-Occe小-d.oL-l=Cd,-c0-c1-C-ced.o

（5）对角矩阵 可逆， 且 注 （1）由定义可知，若 B 是 A 的逆矩阵，则 A 也是 B 的逆矩阵。 （2）设矩阵 A 可逆，则存在唯一的逆矩阵，记为 ，且 （3）矩阵 A 可逆 存在矩阵 B，使得 （4）单位矩阵 I 可逆，且

20al的逆矩阵。例1求矩阵A=82él 2i例如没有逆矩阵A=eoo o1

例1 求矩阵 的逆矩阵。 例如 没有逆矩阵

,则定理2设A，B均是n阶可逆矩阵，数１0(1 )A-I可逆，）=AQAAI=AA=E\A"可逆证明：且有(A) = A.(2)IA可逆，且(IA)=证明：因为 AA-1=A-IA=E所以 (l A)(=A")=(-A)(LA)=E即(I A)

定理2 设 A ，B 均是 n 阶可逆矩阵，数 ，则 （1 ） 可逆，且 （2 ） 可逆，且 证明： 证明：

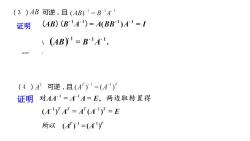
（3）AB可逆，且（AB)=B"A-1(AB) (B-A-")= A(BB-)A-1 =I证明\(AB)"=B-"A-I（4）A 可逆,且（A')-I=(A-")对AAI=AA=E，两边取转置得证明(A') A"=A"(A")" = E所以(A')"=(A")

（3 ） 可逆，且 （4 ） 可逆，且 证明 证明

例2设B2=B，A=I+B，证明：A可逆且 A1=(31é131(I +B)- (I +B)u12证31au222331(I2 +2B + B2)B+1222331R2R222A可逆且A-1=(3L-

例 2 证

A’ - 3A- 10E =0例3设方阵满足方程证明：A和A－4E都可逆，并求出它们的逆矩阵(A- 3E)=E证： A(A-3E)=10E10所以A可逆，且A-1(A- 3E)10A+E(A- 4E)=E(A- 4E)(A+E)=6E6所以A可逆，且A=(A+E)6

例3 设方阵满足方程 证：

主观题设置10分作答

作答 主观题 10分

由A2 - A- 2E =0,A-EE得A(A- E)=2E2A-E且(A - E)A = 2E=EA二2A-EA-1所以2

所以