《线性代数》课程教学资源(讲稿B,高教版)第一章 矩阵及其初等变换 1-2 高斯消元法和矩阵的初等变换

1-2高斯消元法与矩车的初等变换一、高斯消元法二、矩阵的初等变换三、初等矩阵
1-2 高斯消元法与矩阵的初等变换 一、高斯消元法 二、矩阵的初等变换 三、初等矩阵

一、高斯消元法[3x, - x +5x3 =31引例X - x2 +2x =1用消元法解线性方程组X-2x2—X3=2③X -2x2 - x = 2X -2x2 - x = 2Xi-2x2 - x =2③-5②②-1X2 +3x3 = -1X - x+2x =1X, +3x, =-1③-305x2 +8x, =-3-7x, = 23x-X2+5x=310x =7X-2x- x= 21方程组的解为X2 +3x = -1X2 =722X3 =7X3=7
一、高斯消元法 引例 用消元法解线性方程组 2 2 2 1 3 5 3 1 2 3 1 2 3 1 2 3 x x x x x x x x x ① ② ③ 3 5 3 2 1 2 2 1 2 3 1 2 3 1 2 3 x x x x x x x x x ①←→③ ②-① ③-3① 5 8 3 3 1 2 2 2 3 2 3 1 2 3 x x x x x x x 7 2 3 1 2 2 3 2 3 1 2 3 x x x x x x ③-5② ③ 7 1 7 2 3 1 2 2 3 2 3 1 2 3 x x x x x x 方程组的解为 7 2 7 1 7 10 3 2 1 x x x
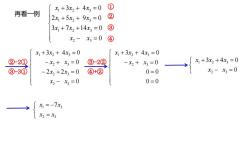
?X+3x2+4x=0再看一例22x +5x2 + 9x =03x, +7x2 +14x = 0X2- Xg= 04X+3x2+4x=0X+3x2+4x3=01+3x2+4x=0②-2@③-2@-X+ =0-X+ X= 0X2-x=0@-30④+②0=0-2x +2x, = 00=0X2- x=0X, =-7xX2=X3
再看一例 0 3 7 14 0 2 5 9 0 3 4 0 2 3 1 2 3 1 2 3 1 2 3 x x x x x x x x x x x ①②③④ ② - 2 ① ③ - 3 ① 0 2 2 0 0 3 4 0 2 3 2 3 2 3 1 2 3 x x x x x x x x x ③ - 2 ② ④ + ② 0 0 0 0 0 3 4 0 2 3 1 2 3 x x x x x 0 3 4 0 2 3 1 2 3 x x x x x 2 3 1 3 7 x x x x

ax+ai2x+...+anx,=b线性方程组的初等变换a2ixj+a22x2+...+a2nx,=b,amXj+am2X2+...+ammx,=b线性方程组的消元法,把方程组化为同解方程组,变换可归结为以下三种形式(1)交换两个方程的位置;(2)用一个非零常数乘某个方程;(3)用一个非零常数乘某个方程然后加到另一个方程
线性方程组的消元法,把方程组化为同解方程组,变换可归结为以下三种形式: (1)交换两个方程的位置; (2)用一个非零常数乘某个方程; (3)用一个非零常数乘某个方程然后加到另一个方程。 线性方程组的初等变换 m m mn n m n n n n a x a x a x b a x a x a x b a x a x a x b 1 1 2 2 2 1 1 2 2 2 2 2 1 1 1 1 2 2 1 1

3x-X2+5x3=3X - x2 +2x; =1X-2x2 - g=2(33)5-1(122(12-2-1-2-1-11-2-r+r112033-1215r, +r0111-1-1-1rr-3r+r30(152,-2(3508-3)(0-7-12)-11210101-20C7XI=77-2-1213r+r1010131-12r, +1177r+rX2=27020120700277X3=7
2 2 2 1 3 5 3 1 2 3 1 2 3 1 2 3 x x x x x x x x x 1 2 1 2 1 1 2 1 3 1 5 3 7 2 7 1 7 10 3 2 1 x x x 3 1 5 3 1 1 2 1 1 2 1 2 1 3 r r 0 5 8 3 0 1 3 1 1 2 1 2 3 1 3 1 2 r r r r 0 0 7 2 0 1 3 1 1 2 1 2 5 2 3 r r 7 2 0 0 1 0 1 3 1 1 2 1 2 7 1 3 r 7 2 0 0 1 7 1 0 1 0 7 12 1 2 0 3 3 1 3 2 r r r r 7 2 0 0 1 7 1 0 1 0 7 10 1 0 0 2 2 1 r r

二、矩阵的初等变换定义1矩阵的行(列)初等变换(1)交换两行(列)的位置;(2)用一个非零数乘某一行(列)的所有元素;(3)用一个非零数乘某一行(列)的所有元素然后加到另一行(列)。rαrj,k,kr+r简记为:行变换列变换C,<>Cj,kc,kc,+Cj
二、矩阵的初等变换 定义1 矩阵的行(列)初等变换 (1)交换两行(列)的位置; (2)用一个非零数乘某一行(列)的所有元素; (3)用一个非零数乘某一行(列)的所有元素然后加到另一行(列)。 i j i i j 简记为:行变换 r r , kr, kr r 列变换 i j i i j c c , k c , k c c

x+3x2+4x=02x +5x2 + 9x,=03x +7x2 +14xg = 0x=0X2-4 133414(1413301-1925110-10-1-2r +r200000014 33r, + r3027-2r2 +r400)0(0(01(000-1)1-1)(107[x =-7k01-13rz +rx=k000(g=k(000J
0 3 7 14 0 2 5 9 0 3 4 0 2 3 1 2 3 1 2 3 1 2 3 x x x x x x x x x x x 0 1 1 3 7 14 2 5 9 1 3 4 0 1 1 0 2 2 0 1 1 1 3 4 3 2 1 3 1 2 r r r r 0 0 0 0 0 0 0 1 1 1 3 4 2 2 4 2 3 r r r r 0 0 0 0 0 0 0 1 1 1 3 4 2 r 0 0 0 0 0 0 0 1 1 1 0 7 3 2 1 r r x k x k x k 3 2 1 7

行阶梯形矩阵行最简形矩阵102-173-1200-727对于一般的线性方程组,AX=b,通过消元法,即对其增广矩阵做三种行初等变换,可将其化为行最简形矩阵,从而进一步讨论方程组解的情况
0 0 7 2 0 1 3 1 1 2 1 2 7 2 0 0 1 7 1 0 1 0 7 10 1 0 0 行阶梯形矩阵 行最简形矩阵 对于一般的线性方程组 ,通过消元法,即对其增广矩阵做三种行初等 变换,可将其化为行最简形矩阵,从而进一步讨论方程组解的情况。 AX b

001d.Cir+1CAn当di±0时,方程组AX=b无解;010..:C2nC2r+1:..d,0001Crr+1CrrA =(A,b) -0dr+当 d=0时,方程组 AX=b的解000000有以下两种情形:x =d,.000000:(1)r=n 时,有唯一解:Jx2=d,xn=d,(2)r<n时,有无穷多个解,X1,X2",X,为基本未知量,Xr+1Xr+2…x,为自由未知量
A (A,b) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 1 0 0 1 1 2 1 2 2 1 1 1 1 r r r r n r r n r n d c c d c c d c c d 当 dr1 0 时,方程组 AX b 无解; 当 时,方程组 的解 有以下两种情形: dr1 0 AX b (1) r n 时,有唯一解: n dn x x d x d 2 2 1 1 (2) r n 时,有无穷多个解, r x , x , , x 1 2 为基本未知量, xr1 , xr2 , , xn 为自由未知量

定理1设n元非齐次线性方程组AX=b对其增广矩阵做行初等变换,化为行最简形矩阵,若d≠0,则方程组无解;若dr+=0,则方程组有解,且当r=n时有唯一解,当r<n时,有无穷多个解。定理2设m个n元方程构成的齐次线性方程组AX=0一定有零解(平凡解),若m<n则方程组一定有非零解
矩阵,若 dr1 0 ,则方程组无解;若 ,则方程组有解,且当 时有唯 AX b r n 一解,当 r n 时,有无穷多个解。 定理1 设 n 元非齐次线性方程组 ,对其增广矩阵做行初等变换,化为行最简形 dr1 0 定理2 设 m 个 n 元方程构成的齐次线性方程组 AX 0 一定有零解(平凡解),若 m n ,则方程组一定有非零解
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《线性代数》课程教学资源(讲稿B,高教版)第一章 矩阵及其初等变换 1-1 矩阵及其运算.pdf
- 《高等数学》课程教学资源(课件讲稿)第1章 第1讲 函数.pdf
- 《线性代数》课程教学资源(章节讲稿,C)3-4 线性方程组解的结构新.pdf
- 《线性代数》课程教学资源(章节讲稿,C)3-3 向量组的秩与极大无关组.pdf
- 《线性代数》课程教学资源(章节讲稿,C)3-2 向量组的线性相关性.pdf
- 《线性代数》课程教学资源(章节讲稿,C)3-1 n维向量空间的概念.pdf
- 《线性代数》课程教学资源(章节讲稿,C)2-5 矩阵的秩.pdf
- 《线性代数》课程教学资源(章节讲稿,C)2-4 克拉默法则.pdf
- 《线性代数》课程教学资源(章节讲稿,C)2-3 拉普拉斯定理.pdf
- 《线性代数》课程教学资源(章节讲稿,C)2-2 n阶行列式的性质与计算.pdf
- 《线性代数》课程教学资源(章节讲稿,C)2-1 n阶行列式的定义.pdf
- 《线性代数》课程教学资源(章节讲稿,C)1-4 分块矩阵.pdf
- 《线性代数》课程教学资源(章节讲稿,C)1-3 逆矩阵.pdf
- 《线性代数》课程教学资源(章节讲稿,C)1-2 高斯消元法和矩阵的初等变换.pdf
- 《线性代数》课程教学资源(章节讲稿,C)1-1 矩阵及其运算.pdf
- 《高等数学》课程教学资源(课件讲稿)第3章 第3讲 泰勒中值定理.pdf
- 《高等数学》课程教学资源(课件讲稿)第3章 第3讲 泰勒中值定理.pdf
- 《高等数学》课程教学资源(课件讲稿)第3章 第2讲 洛必达法则.pdf
- 《高等数学》课程教学资源(课件讲稿)第3章 第1讲 微分中值定理.pdf
- 《高等数学》课程教学资源(课件讲稿)第2章 第4讲 函数的微分.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第一章 矩阵及其初等变换 1-3 逆矩阵.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第一章 矩阵及其初等变换 1-4 分块矩阵.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第三章 n维向量空间 3-1 n维向量空间的概念.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第二章 行列式 2-1 n阶行列式的定义.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第二章 行列式 2-2 n阶行列式的性质与计算.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第二章 行列式 2-3 拉普拉斯定理.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第二章 行列式 2-4 克拉默法则.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第二章 行列式 2-5 矩阵的秩.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第三章 n维向量空间 3-2 向量组的线性相关性.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第三章 n维向量空间 3-3 向量组的秩与极大无关组.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第三章 n维向量空间 3-4 线性方程组解的结构.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第四章 特征值与特征向量 4-1 特征值与特征向量的概念与计算.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第四章 特征值与特征向量 4-2 矩阵的相似对角化.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第四章 特征值与特征向量 4-3 n维向量空间的正交性.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第四章 特征值与特征向量 4-4实对称矩阵的相似对角化.pdf
- 《高等数学》课程教学资源(课件讲稿)第1章——第1节映射与函数.pdf
- 《高等数学》课程教学资源(课件讲稿)第1章——第2节数列的极限.pdf
- 《高等数学》课程教学资源(课件讲稿)第1章——第10节闭区间上连续函数的性质.pdf
- 《高等数学》课程教学资源(课件讲稿)第1章——第3节函数的极限.pdf
- 《高等数学》课程教学资源(课件讲稿)第1章——第4节无穷小与无穷大.pdf
