《高等数学》课程教学资源（课件讲稿）第3章 第3讲 泰勒中值定理

高等数学（上册）第3章微分中值定理与导数的应用第3讲泰勒中值定理1人民邮电出版社POSIS&TELECOMPRESS

高等数学（上册） 第3讲 泰勒中值定理 第3章 微分中值定理与导数的应用

R人邮教育本讲内容w.nyjiaoyu.co泰勒中值定理0102麦克劳林公式03几个重要初等函数的麦克劳林公式04泰勒公式的应用

01 泰勒中值定理 02 麦克劳林公式 03 几个重要初等函数的麦克劳林公式 04 泰勒公式的应用 本 讲 内 容

01泰勒中值定理COAORA人邮教育在微分应用中已知近似公式：Vf(x)= f(x)+ f(x)(x-x)y=f(x)P(x)p(x)x的一次多项式XXox特点：p(x)= f(x)以直代曲p'(x)=f(x)如何提高精度？需要解决的问题如何估计误差？

01 泰勒中值定理 特点: 在微分应用中已知近似公式 : 需要解决的问题 如何提高精度 ? 如何估计误差 ? x 的一次多项式 0 0 0 f (x)  f (x )  f (x )(x  x ) 1 p (x) 1 0 0 p (x )  f (x ) 1 0 0 p '(x )  f '(x )

01泰勒中值定理COAOR人邮教育定理3.6（泰勒中值定理）设函数f(x)在含有xo的某个开区间(a,b)内具有直到(n+1)阶导数,则对任意xE(a,b)有f(x）按x-x.的幂展开的带有lagrange型余项n阶Taylor公式f"(x)f(x)= f(x)+ f'(x)(x-xx--x)2!H(x)(x- x)" + R(x)(3.1)n!C其中R.(x)(n +1)!拉格朗日型余项其中介于x与x之间

则对任意 x(a,b) 有 定理3.6 (泰勒中值定理) 设函数 f (x)在含有x0的某个开区间 (a,b)内具有直到(n 1) ( 1) 1 0 ( ) ( ) ( ) ( 1)! n n n f R x x x n       其中 , 0 2 0 0 0 0 ( ) ( ) ( ) ( )( ) ( ) 2! f x f x f x f x x x x x        ( ) 0 0 ( ) ( ) ( ) ! n n n f x x x R x n    (3.1) 其中ξ介于x0与x之间. 拉格朗日型余项 阶导数, 01 泰勒中值定理 4 0 ( )  的幂展开的带有lagrange型 余项n阶Taylor公式 f x 按x x

1. 求 n次近似多项式 Pn(x),要求：Pn(xo)= f(xo), Ph(xo)= f'(xo), , pm(xo)= f(n)(xo)Pn(x)=ao+ai(x-xo)+a2(x-xo)? +...+ an(x-xo)n令ai+ 2a2(x-xo)+..+nan(x-xo)n-l则 pn(x)=ph(x) =2!a2+..+n(n-1)an(x-xo)n-2p("(a)=n!anaj = pn(xo)= f'(xo)ao = Pn(xo)= f(xo),a2 =ph(xo)="(xo), ,an =pm(xo)= f(n)(xo)故 Pn(x)= f(xo)+ f(xo)(x-xo)+2f"(xo)(x-xo)2十+ (m)(x0)(x-x0)"HIGH EDUCATION PRESSA非云

1. 求 n 次近似多项式 要求: 故 机动 目录 上页 下页 返回 结束 令 则

2.余项估计令 R,(x)=f(x)-Pn(x)(称为余项)，则有R,(xo)= R′(xo) =...= R(n)(xo) = 0R,(x)(x-xo)n+R,(5)R,(x)-R,(xo)(Si在Xo与x之间)(x-xo)n+1_0(n+1)(i-xo)nR"(52)R,() -R'(xo)(52 在Xo与(n + 1)(5i - xo)"-0 ~ (n+ 1)n(52 - xo)n-1引之间)R(n"(E,)-Rm(xo)_ R(n+)(E)(在x与x之间)(n+l)!(n +1)...2(En -xo)-0HIGH EDUCATION PRESS返向

2. 余项估计 令 (称为余项) , 则有 机动 目录 上页 下页 返回 结束

CO00R人邮教育"x.(xp,(x)= f(x)+ f'(x)(x-x)+2!n!f(x）在x处的n阶泰勒多项式f(x)在x,处展开的泰勒系数k!

7 0 2 0 0 0 0 ( ) ( ) ( ) ( )( ) ( ) 2!  n       f x p x f x f x x x x x ( ) 0 0 ( ) ( ) !   n n f x x x n ( ) 0 ( ) !  k k f x a k 0 f ( x)在x 处的n阶泰勒多项式 0 f (x)在x 处展开的泰勒系数

01泰勒中值定理COAO人邮教育PS拉格朗日型余项1+2n+R,(x) :(在xo与x之间)x-xo(n+1)!佩亚诺型的余项f(n+l)()M)+R(x)(n+1)!(n + 1)!R,(x)lim0，及即 R,(x)=o[(x-x)"佩亚诺型余项x-→xo(x-o.-(x.所以f(x)=x-x)*+o[(x-x)"]k!k=0

佩亚诺型余项 ( 1) 1 0 ( ) ( ) ( ) ( 1)! n n n f R x x x n       (ξ在x0与x之间) 拉格朗日型余项 佩亚诺型的余项 即 0 ( ) [( ) ] n Rn 及 x  o x  x 0 0 ( ) lim 0, ( ) n n x x R x  x x   ( 1) 1 1 0 0 ( ) ( ) ( ) ( ) ( 1)! ( 1)! n n n n f M R x x x x x n n          ≤ 所以 ( ) 0 0 0 0 ( ) ( ) ( ) [( ) ] ! k n k n k f x f x x x o x x  k      01 泰勒中值定理 8

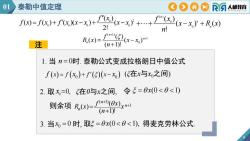
01泰勒中值定理CO人邮教育RAf"(x)f("(x)f(x)= f(x)+ f(x)(x-x)+(x-x)"+R(x)2!n!f(n+l)D（)x.)n+R(x):注(n+1)!1.当n=0时.泰勒公式变成拉格朗日中值公式f(x)=f(x)+f()(x-xo) (在x与xo之间)2. 取×=0,在0与x之间，令=x(0<0<1)则余项 R,(x)=()(@x)x+1(n+1)!3. 当x=0 时,取=0x(0<0<1),得麦克劳林公式

注 1. 当 n  0时. 泰勒公式变成拉格朗日中值公式 3. 当 时, 0 x  0 (ξ在x与x0之间) ξ在0与x之间, 则余项 ( 1) 1 ( ) ( ) ( 1)! n n n f x R x x n      0 2 x 0, . 取 令   x(0  1) 取  x(0  1), 得麦克劳林公式. 01 泰勒中值定理 9        0 0 f x  f x  f   x  x 0 2 0 0 0 0 ( ) ( ) ( ) ( )( ) ( ) 2! f x f x f x f x x x x x        ( ) 0 0 ( ) ( ) ( ) ! n n n f x x x R x n    ( 1) 1 0 ( ) ( ) ( ) ( 1)! n n n f R x x x n      

R人邮教育本讲内容w,nyjiaoyu.c01泰勒中值定理02麦克劳林公式03几个重要初等函数的麦克劳林公式04泰勒公式的应用

01 泰勒中值定理 02 麦克劳林公式 03 几个重要初等函数的麦克劳林公式 04 泰勒公式的应用 本 讲 内 容