《高等数学》课程教学资源（课件讲稿）第3章 第3讲 泰勒中值定理

高等数学（上册）第3章微分中值定理与导数的应用第3讲泰勒中值定理人民邮电出版社POSTS&TELECOMPRESS

高等数学（上册） 第3讲 泰勒中值定理 第3章 微分中值定理与导数的应用

R人邮教育本讲内容w.nvliaDyu.c泰勒中值定理02麦克劳林公式03几个重要初等函数的麦克劳林公式04泰勒公式的应用

01 泰勒中值定理 02 麦克劳林公式 03 几个重要初等函数的麦克劳林公式 04 泰勒公式的应用 本 讲 内 容

01泰勒中值定理COAOR人邮教育在微分应用中已知近似公式：f(x)》 f(x)+ fdx)(x- x)Vy=f(α)P(x)p(x)x的一次多项式Xxox特点：以直代曲p(x)= f(x)p (x)= f(x)如何提高精度？需要解决的问题如何估计误差？

01 泰勒中值定理 特点: 在微分应用中已知近似公式 : 需要解决的问题 如何提高精度 ? 如何估计误差 ? x 的一次多项式

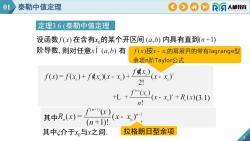
01泰勒中值定理COAOR人邮教育定理3.6（泰勒中值定理设函数f(x)在含有x.的某个开区间(a,b)内具有直到(n+1)阶导数,则对任意xl（a,b）有f(x）按x-x.的幂展开的带有lagrange型余项n阶Taylor公式faxf(x)= f(x)+ fdx)(x- xX2!(r.+(x - x)" + R,(x)(3.1)n!其中R,(x)(n +1)!拉格朗日型余项其中介于x与x之间

则对任意 有 定理3.6 (泰勒中值定理 )设函数 在含有x0的某个开区间 内具有直到 其中 , (3.1) 其中ξ介于x0与x之间. 拉格朗日型余项 阶导数, 01 泰勒中值定理 4

OO00人邮教育RAfaxXp,(x)= f(x)+ fdx)(x- x)+2!n!f(x)在x.处的n阶泰勒多项式f(x)在x.处展开的泰勒系数k!

7

01泰勒中值定理COAORA人邮教育拉格朗日型余项n+1)xR,(x)x.)n+(在xo与x之间)(n+I)!佩亚诺型的余项Mr(n+)(xR, (x)(n +1)!(n + I)!R,(x)lim0.及即 R,(x)=o[(x- x)"]佩亚诺型余项XRXo(X-所以f(x)=a(x- x)"+o[(x- x)"]k!0

佩亚诺型余项 (ξ在x0与x之间) 拉格朗日型余项 佩亚诺型的余项 及 即 所以 01 泰勒中值定理 8

01泰勒中值定理CO0RA人邮教育fax))+L +"(x)f(x)= f(x)+ fdx)(x- x)(x- x)"+R(x)2!n!f(n+1)(x)R,(x) =(x- x)"*注(n +1)!1.当n=0时.泰勒公式变成拉格朗日中值公式f(xr)=f(xo)+ fdx)(x- xo） (在x与xo之间)2. 取x=0. 在0与x之间，令x =qx(0<q<1)则余项 R,(x)=u)(g)x-1(n+1)!3.当x=0 时,取x=qx(0<q<1),得麦克劳林公式

注 1. 当 时. 泰勒公式变成拉格朗日中值公式 3. 当 时, (ξ在x与x0之间) ξ在0与x之间, 则余项 2. 取 令 取 得麦克劳林公式. 01 泰勒中值定理 9

R人邮教育本讲内容W,nvlaDyu.c01泰勒中值定理02麦克劳林公式03几个重要初等函数的麦克劳林公式04泰勒公式的应用

01 泰勒中值定理 02 麦克劳林公式 03 几个重要初等函数的麦克劳林公式 04 泰勒公式的应用 本 讲 内 容

02麦克劳林公式COA0人邮教育RA定理3.7设函数f(x）在含有x=0的某个开区间(a,b）内具有直到(n+1)阶导数,则对任意xl (a,b)有f(x)=f(0)+ fα0)x+2() x2 ++(ax)xn+1 (0<g<1)(3.5)n!(n +1)!称为函数f(x)的n阶带拉格朗日型余项的麦克劳林公式(x)=f(0)+ fα0)+2()x2+L +f(n)(0)2xn+0(x") (3.6)21n!称为带佩亚诺余项的n阶麦克劳林公式

定理3.7 称为带佩亚诺余项的n阶麦克劳林公式. 设函数 在含有 的某个开区间 内具有直到 称为函数 的n阶带拉格朗日型余项的麦克劳林公式. (3.6) 阶导数,则对任意 有 (3.5) 02 麦克劳林公式 11

02麦克劳林公式COAO人邮教育RA由(3.5)和(3.6)可得近似公式(x)> f(0)+ f 0)x+F(0)x2 +L + f(n)(0)rf2!n!右端多项式记作：P,(x)= f(0)+ f 0)+2(0) x2 +L + f("(0) xn21n!称为f(x)的n阶麦克劳林多项式.其系数为f(k)(O)(k=0,1,2,L n)Lkn+1MR,(x)≤误差估计式(n+1)

称为 的n阶麦克劳林多项式, 其系数为: 由(3.5)和(3.6)可得近似公式 右端多项式记作: 误差估计式: 02 麦克劳林公式 12