《线性代数》课程教学资源（章节讲稿，C）3-1 n维向量空间的概念

第三章n维向量空间3-1n维向量空间的概念3-2可量组的线性相关性3-3向量组的秩与极大无关组3-4线性方程组解的结构

第三章 n 维向量空间 3-1 n 维向量空间的概念 3-2 向量组的线性相关性 3-3 向量组的秩与极大无关组 3-4 线性方程组解的结构

3-1n维向量空间的概念引入1°空间直角坐标系中，向径OP是一个三维向量，坐标表为（aj,α2,a）2ao0(o30203)212°矩阵的每一行元素可以构成一个）-304 -行矩阵2 #80(010102）a0o2a002e3 0::CC：C每一列元素可以构成一个列矩阵c0- c4-1, c-3-,208102008203°n元线性方程a+α+L+a,x=b的系数可以记为(aj,a,,L,an)

3-1 n 维向量空间的概 引入 念 1°空间直角坐标系中，向径 是一个三维向量，坐标表示为 2°矩阵 的每一行元素可以构成一个 行矩阵 每一列元素可以构成一个列矩阵 3° n 元线性方程 的系数可以记为

一、向量及向量空间定义1称为数域P上的n个数组成的有序数组a=（a,αz,L,an）量。ea, o注号Ccaz-列（1）行向量：（a,αz,L，a）+SL向量：a.(2) a,称为向量的分量 1,2,L ,n)（3）设向量a=（a,az,L,a),b=(b,bz,L,b)α =b (i=1,2,L,n)，则称向量相等：0 =(0,0,L ,0)（4）零向量量-a=(-aj,-az,L ,-a)（5）负向量

定义1 数域 P上的 n 个数组成的有序数组 称为一个 n 维向 量。 （1）行向量： 列 向量： （2） 称为向量的分量 （3）设向量 ，若 ，则称向量相等： 注 （4）零向量 （5）负向量 一、向量及向量空间

定义2（向量的线性运算）设向量a =(aj,a2,L,a,),b=(b,b,L,b,), ki P（数域）a +b =(a +b,az +b,,L ,a,+b.)向量加法数乘向量ka =(kaj,ka,,L ,ka,)定义3 Rn)（n维实向量空间全体n维向量的集合，对于加法和数乘运算封闭，且满足下列运算规律：(5) la =α;(l) a +b =b+a;(6) k(la )= (kl)a ;(2) (a +b)+g =a +(b +g);(3) α +0=a;(7) k(a +b)=ka +kb;(4) a +(-a)=0;(8) (k +1)a = ka +la

定义2 （向量的线性运算） 设向量 （数域） 向量加法 数乘向量 定义3 （ n 维实向量空间 Rn） 全体 n 维向量的集合，对于加法和数乘运算封闭，且满足下列运算规律：

ianx+azx,+L +anx,=ba21xj +a22x2+L +a2nx,=b,可记为向量方程：例如，n元线性方程组LLLiamx+am2x2+L+ammx,=b,aeai2 0a ?ain hoBCcOC卡.0ca2n-ga2caxa,+xa,+L +x,a,=b+1+XnCX2XiCM.SMMMAM··小ean小eaotaeaex, o:cc:X=或 xa,+xa+L +x,a,=(a,a,,L a,)X=b（解向量）SM8Sxno

例如，n 元线性方程组 可记为向量方程： 或 （解向量）

线性方程组的向量表示a12x2+Lbr,ainanxiXna22X2+Lb2,a2nxna21 x1L1LLLTLT工1am1.xi+am2X2+LbmamXn16T比+ax.1aS

线性方程组的向量表示

子空间二定义4（R"的子空间）非空向量集合VIR”，如果V对于R"的线性运算也构成一个向量空间，则称V为R"的一个子空间。定理1非空子集V是R"的子空间一V对于加法和数乘运算封闭例1在3维向量空间R3中，定义两个子集：V =((x),X2,x,)|x +x2 +x =0)是 R的子空间V, ={(x),x2,x) x, +x2 +x, =1)不是R的子空间

定义4 （ Rn 的子空间） 二、 子空间 非空向量集合 ，如果 对于 的线性运算也构成一个向量空间，则 称 为 的一个子空间。 定理1 非空子集 是 的子空间 对于加法和数乘运算封闭 例1 在3维向量空间 中，定义两个子集： 是 的子空间 不是 的子空间

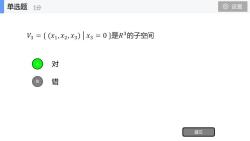
单选题设置1分V=（（×1,×2,×3）x3= 0}是R3的子空间对错提交

对 错 A B 提交 单选题 1分

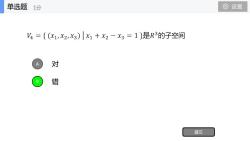
单选题设置1分V4=（（×1,23）×1+×2×3=1是R3的子空间对错提交

对 错 A B 提交 单选题 1分