《线性代数》课程教学资源（讲稿B，高教版）第三章 n维向量空间 3-4 线性方程组解的结构

3-4线性方程组解的结构、齐次线性方程组-ax +ai2x2 +..+ainx, = 0即 AX=0a21x +a22x2 +...+a2nxn =0amX,+am2X2+...+ammX,=0已有结论：1°AX=0 必有零解：2°R(A)=n AX=0只有零解A的列向量组线性无关3°R(A)<n A的列向量组线性相关AX =0 有非零解食

3-4 线性方程组解的结构 一、齐次线性方程组                    0 0 0 1 1 2 2 2 1 1 2 2 2 2 1 1 1 1 2 2 1 m m mn n n n n n a x a x a x a x a x a x a x a x a x     即 AX  0 已有结论： 1° AX  0 必有零解： 2° AX  0 只有零解 R(A)  n A 的列向量组线性无关 3° AX  0 有非零解 R(A)  n A 的列向量组线性相关

齐次方程组解的性质性质1若 、≤2是齐次方程组 AX =0 的解，则i +≤2 也是 AX=0的解。性质2若是齐次方程组AX=0的解，任意数k,则kE也是AX=0的解性质3若、,、、是齐次方程组AX=0的解，任意s个数k、k,、、k、k+k52+...+k..也是AX=0的解。齐次方程组AX=0的全体解的集合称为AX=0的解空间，解空间的任一定义组基称为AX=0的一个基础解系注解向量S、S2、、、是AX=0的一个基础解系一→5、2、、，线性无关，且任一解向量都可由它线性表示

齐次方程组解的性质 性质1 若 1 、 2 是齐次方程组 AX  0 的解，则 1  2 也是 AX  0 的解。 性质2 若  是齐次方程组 AX  0 的解，任意数 k, 则 k 也是 AX  0 的解。 性质3 若 是齐次方程组 的解，任意 个数 ， 也是 的解。 1 、 2 、、 s AX  0 AX  0 s s k 、k 、、k 1 2 s s k1 1  k2  2  k  定义 齐次方程组 的全体解的集合称为 的解空间，解空间的任一 组基称为 的一个基础解系。 AX  0 AX  0 AX  0 注 解向量 1 、 2 、、 s 是 AX  0 的一个基础解系 1 、 2 、、 s 线性无关，且任一解向量都可由它线性表示

设齐次方程组 AX=0 的系数矩阵 A的秩R(A)=r<n，则方程组 AX=0 的定理基础解系含n一r个解向量。证明设R(A)=r，不妨设A的前r个列向量线性无关，于是A的行最简形为01bir+bun0brn1b..B :000000x, =bir+ixr+1 +...+binx,与B相对应的线性方程组为(1)X,=brr+iXrt1+...+brnx

定理 设齐次方程组 AX  0 的系数矩阵 A 的秩 R(A)  r  n ，则方程组 AX  0 的 基础解系含 n r 个解向量。 证明 设 R(A)  r ，不妨设 A 的前 r 个列向量线性无关，于是 A 的行最简形为                        0 0 0 0 0 0 0 1 1 0 1 1 1 1                   r r r n r n b b b b B 与 B 相对应的线性方程组为                r r r r r n n r r n n x b x b x x b x b x 1 1 1 1 1 1 1    （1）

X, =bi++r++.+bi'x.显然，方程组AX=0与方程组（1）同解[x, =brr+1Xr+I +...+brnxn任给xr+1，",xn一组值，则唯一确定Xi,X2，,X的值，即得方程组（1）的一个解，也是方程组AX=0的-J一个解称xr+1，",x，为自由未知量(0)01+r+l001Xr+2若令xr+1,",x,取n-r组数：:.010x.(-binx由（1)得..(-brnxr+2

显然，方程组 AX  0 与方程组（1）同解。                r r r r r n n r r n n x b x b x x b x b x 1 1 1 1 1 1 1    任给 xr1 ,  , xn 一组值，则唯一确定 x1 , x2 ,  , xr 的值， 即得方程组（1）的一个解，也是方程组 AX  0 的一个解。 称 xr1 ,  , xn 为自由未知量， r n x , , x 1  n r                                                            1 0 0 , , 0 1 0 , 0 0 1 2 1      n r r x x x 由（1）得 若令 取 组数：                                                    r n n r r r r r r r b b b b b b x x 1 2 1 2 1 1 1 1   ,  ,, 

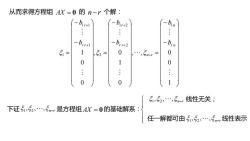
从而求得方程组AX=0的n-r个解：(-br+1)(br+2:::-brn-br+1-brr+20025=1,52 =001......:00151,52,,5-, 线性无关;下证S152，…，,-是方程组AX=0的基础解系：任一解都可由5,52，,5n-,线性表示-

从而求得方程组 AX  0 的 n r 个解：                                                                                 1 0 , , 0 0 1 , 0 0 0 1 1 2 1 2 2 1 1 1 1        r n n n r r r r r r r b b b b b b    下证 1 , 2 ,  , nr 是方程组 AX  0 的基础解系： 1 , 2 ,  , nr 线性无关；   任一解都可由 线性表示       nr , , , 1 2 

设方程组AX=0的任一解=（,,+,）作向量n=r+1S++22+.+,n-r，由解的性质可知，n是方程组AX=0的解，比较n与的后n-r个分量对应相等，由方程组（1）知，前r个分量也必然相等，因此 n=≤证毕即可由,5，,线性表示。X=k+kz52++kn-rsn-r（k,k2,,kn-r为任意常数）齐次方程组的通解求通解的步骤：系数矩阵行最简形—自由未知量—基础解系—通解

设方程组 的任一解  AX  0 T r r n ( , , , , , )   1    1   作向量   r1 1 r2  2 n  nr ， 由解的性质可知， 是方程组 AX  0 的解， 比较  与  的后 n r 个分量对应相等，由方程组（1）知，前 r 个分量也必然相等， 因此   即  可由 1 , 2 ,  , nr 线性表示。 证毕 n r n r X k k k 齐次方程组的通解  1 1  2  2     n r k k k  , , , （ 1 2  为任意常数） 求通解的步骤： 系数矩阵 行最简形 自由未知量 基础解系 通解

2x, +X2-2x, + 3x4=0的通解。例1求齐次线性方程组13x, +2x2-X;+2x4=0(X++-=0解：对系数矩阵进行初等行变换，/3(1 (11(104 211 -1-31 -2-112504-53223-120A=-1-1-4-→→5000(23(001-111-2-1-4X =3x -4x4秩为2，基础解系含2个解向量，取自由未知量x3，X4，得同解方程组[x2 =-4x +5x43(-4)5-4基础解系=通解为X=k5i+k252kj,k2为任意常数1001

例1 求齐次线性方程组 的通解。                  0 3 2 2 0 2 2 3 0 1 2 3 4 1 2 3 4 1 2 3 4 x x x x x x x x x x x x 解：对系数矩阵进行初等行变换，               1 1 1 1 3 2 1 2 2 1 2 3 A               2 1 2 3 3 2 1 2 1 1 1 1                 0 1 4 5 0 1 4 5 1 1 1 1              0 0 0 0 0 1 4 5 1 0 3 4 秩为 2，基础解系含 2 个解向量，取自由未知量 x3 , x4 ，得同解方程组                                1 0 5 4 , 0 1 4 3 基础解系 1  2         2 3 4 1 3 4 4 5 3 4 x x x x x x 通解为 1 2 ， k , k 1 1 2  2 X  k  k 为任意常数

X+x2-3x-x4=0例2求齐次线性方程组的基础解系。3x -X2 -3x, +4x4 =0X+5x2-9xg-8x4=0解：对系数矩阵进行初等行变换，CA-3-11(11-3(111-1)(11-3-1-1-337104677-16→A=3-30-404↓-→124501(0-84(000-90-6-70003301243710秩为2基础解系含2个解向取自由未知量X3,X4240(3)60003316x, =X3x4P2C基础解系得同解方程组0473xx0424

例2 求齐次线性方程组 的基础解系。                  5 9 8 0 3 3 4 0 3 0 1 2 3 4 1 2 3 4 1 2 3 4 x x x x x x x x x x x x 解：对系数矩阵进行初等行变换，                  1 5 9 8 3 1 3 4 1 1 3 1 A 秩为 2，基础解系含 2 个解向量，取自由未知量 x3 , x4 ，                               4 0 7 3 , 0 4 6 6 基础解系 1  2            2 3 4 1 3 4 4 7 2 3 4 3 2 3 x x x x x x                 0 4 6 7 0 4 6 7 1 1 3 1               0 0 0 0 0 4 6 7 1 1 3 1                  0 0 0 0 4 7 2 3 0 1 1 1 3 1                     0 0 0 0 4 7 2 3 0 1 4 3 2 3 1 0 得同解方程组

求解齐次线性方程组的步骤：初等行变换1) 将A-（行最简形）2）写出与原方程组同解的方程组X =-ki,r+1Xr+1 -...- kinxnX, =-kr,r+1Xr+1 -...-kmXn

求解齐次线性方程组的步骤： 1 0 0 r I B A       ） 将 初等行变换 （行最简形） 2）写出与原方程组同解的方程组：      r r r r rn n x  k x   k x , 1 1  r r n n x k x k x 1   1, 1 1  1 

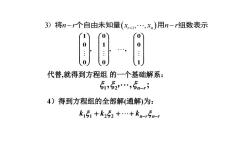
3）将n-r个自由未知量(xr+1,,x）用n-r组数表示(0)1000.(1）00代替,就得到方程组的一个基础解系：S1,S2,.",5n-r;4）得到方程组的全部解（通解)为：ki5i +k,52 +...+kn-r5n-r

                                          1 0 0 , , 0 1 0 , 0 0 1     代替,就得到方程组 的一个基础解系： 4）得到方程组的全部解(通解)为： 1 2 , , ; n r    ，  n r n r k k k 1  1  2  2     3 , , ）将n r x x n r   个自由未知量 r n 1 用 组数表示