《高等数学》课程教学资源（课件讲稿）第1章——第5节极限运算法则

第一章 第五节 极限运算法则 无穷小运算法则 二、 极限的四侧运算法则 三、复合函数的极限运算法则 HIGH EDUCATION PRESS 机动目录上页下页返回结束

第一章 二、 极限的四则运算法则 三、 复合函数的极限运算法则 一 、无穷小运算法则 第五节 机动 目录 上页 下页 返回 结束 极限运算法则

一、无穷小运算法则 定理1.有限个无穷小的和还是无穷小 证：考虑两个无穷小的和.设1ima=0,lim阝=0， x→x0 x→x0 V6>0,381>0,当00,当0<x-x<δ2时，有f< 取8=min{ò1，d2,则当0<x-xo<δ时，有 a+B≤a+B<号+号=& 因此 lim(a+β)=0. x→x0 这说明当x→x时，a+B为无穷小量 HIGH EDUCATION PRESS 机动目录上页下页返回结束

 = min 1 ,  2 , 时, 有 一、 无穷小运算法则 定理1. 有限个无穷小的和还是无穷小 . 证: 考虑两个无穷小的和 . 设   0, 当 时 , 有 当 时 , 有 取 则当  −   0 0 x x  +    +  2 2    + =  因此 这说明当 时, 为无穷小量 . 机动 目录 上页 下页 返回 结束

类似可证：有限个无穷小之和仍为无穷小 说明：无限个无穷小之和不一定是无穷小！ 例如， lim 2十.+ n->0 HIGH EDUCATION PRESS 机动目录上页下页返回结束

说明: 无限个无穷小之和不一定是无穷小 ! 例如，       + + + + + → n + n  n n n n 2 2 2 1 2 1 1 lim  机动 目录 上页 下页 返回 结束 类似可证: 有限个无穷小之和仍为无穷小

定理2.有界函数与无穷小的乘积是无穷小 证：设Vx∈U(x,δ)，u≤M 又设lima=0,即e>0,382>0,当x∈U(x,δ2) x→x0 时，有a≤号 取δ=min{8,δ2)，则当xeU(x,δ)时，就有 ua=ua≤M.8=e 故lim ua=0,即uc是x→xo时的无穷小 x→x0 推论1.常数与无穷小的乘积是无穷小 推论2.有限个无穷小的乘积是无穷小 HIGH EDUCATION PRESS 机动目录上页下页返回结束

定理2 . 有界函数与无穷小的乘积是无穷小 . 证: 设 u  M 又设 lim 0, 0 = →  x x 即   0, 当 时, 有 M    取 min , , 1 2  =   则当 ( , ) x x0    时 , 就有 u = u      = M M 故 即 是 时的无穷小 . 推论 1 . 常数与无穷小的乘积是无穷小 . 推论 2 . 有限个无穷小的乘积是无穷小 . 机动 目录 上页 下页 返回 结束

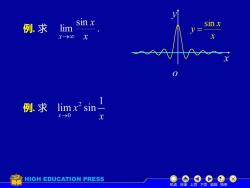
例.求 lim sinx sinx V= x→00 例求 i limx"sin x->O HIGH EDUCATION PRESS 机动目录上页下页返回结束

例. 求 x x y sin = 机动 目录 上页 下页 返回 结束 例. 求

二、极限的四则运算 定理若limf(x)=A,1img(x)=B,则有 (I)1im[f(x)±g(x]=limf(x)±limg(x)=A±B (2)lim[f(x)g(x)]=lim f(x)lim g(x)=4B (3)lim()=limf(x)4 g(x) limg(x)B (B≠0) HIGH EDUCATION PRESS 机动目录上页下页返回结束

二、极限的四则运算 lim f (x) = A, lim g(x) = B , 机动 目录 上页 下页 返回 结束 （B≠0） 定理 若 则有

推论.若limf(x)存在且1imf(x)=A,则有 ()lim[cf(x)]=climf(x)=cA(c为常数) (2)lim[f(x)]”=[limf(x)]”=A”(n为正整数) 推论：若limf(x)=A,limg(x)=B,且f(x)≥g(x), 则A≥B. 提示：令p(x)=f(x)-g(x) HIGH EDUCATION PRESS 机动目录上页下页返回结束

推论 . 若 lim ( ) f x 存在 则有 (1 lim[ ( )] lim ( ) ) cf x c f x cA = = ( c 为常数 ) (2 lim[ ( )] [lim ( )] ) n n n f x f x A = = ( n 为正整数 ) 机动 目录 上页 下页 返回 结束 且lim ( ) , f x A = 推论: 若 lim f (x) = A, lim g(x) = B, f (x)  g(x), A B . 提示: 令 (x) = f (x) − g(x) 且 则

设n次多项式Pn(x)=ao+ax+.+anx”, limP,(x)=a0+a,limx+.+a,lim x”=Pn(xo)》 x→x0 x->x0 x→x0 设有分式函数R(x)= P() 2(x) 其中P(x),Q(x)都是 多项式，若Q(x)≠0，则 lim P(x) lim R(x)= X→x0 P(xo) R(Xo) x→x0 lim O(x) e(xo) x→x0 说明：若Q(xo)=0,不能直接用商的运算法则 HIGH EDUCATION PRESS 机动目录上页下页返回结束

设有分式函数 其中 都是 多项式 , 则 = → lim ( ) 0 R x x x lim ( ) lim ( ) 0 0 Q x P x x x x x → → 说明: 若 不能直接用商的运算法则 . 若 机动 目录 上页 下页 返回 结束 设 n 次多项式 = → lim ( ) 0 P x n x x

定理6.若1imxn=A,lim y=B,则有 n>00 n→oo ()lim(xn±yn)=A±B n-→0 (2) lim xnyn=AB n>o∞ (3)当yn≠0且B≠0时，1imn= n-o yn B HIGH EDUCATION PRESS 机动目录上页下页返回结束

定理6 . 若 lim x A, lim y B , n n n n = = → → 则有 (1) lim( ) n n n x  y → n n n x y → (2) lim (3) 当y  0且 B  0时, n B A y x n n n = → lim = A  B = AB 机动 目录 上页 下页 返回 结束

例.求lim x-3 3x2-9 例.lim x2+2x+c 求c x→1 x-1 x-1 例.求lim x1x-1 HIGH EDUCATION PRESS OeOC®8 机动目录上页下页返回结束

例. 求 机动 目录 上页 下页 返回 结束 例. 求 c 例 . 求