《线性代数》课程教学资源(讲稿B,高教版)第二章 行列式 2-1 n阶行列式的定义

第二章行列式2-1n阶行列式的定义2-2行列式的性质和计算2-3拉普拉斯定理2-4克拉默法则2-5矩阵的秩
第二章 行列式 2-1 n 阶行列式的定义 2-2 行列式的性质和计算 2-3 拉普拉斯定理 2-4 克拉默法则 2-5 矩阵的秩

2-1n阶行列式的定义aiix +ai2x, =b考虑二元线性方程组[a2 +a22x =b,b,a22 -ai2b2xa22-a221当aa22一za±0时,则方程组的解为a,bz -b,a21X2ai22 -ai221b,hd12aa12d记矩阵A:Ab,ba22a21a21a-01ai1a12称为一个二阶行列式,且aα22-ai221= det A=Aa22a21a22[a21
2-1 n 阶行列式的定义 2 1 1 2 2 2 2 1 1 1 1 2 2 1 a x a x b a x a x b 考虑二元线性方程组 当 a1 1a2 2 a1 2a2 1 0 时,则方程组的解为 1 1 2 2 1 2 2 1 1 1 2 1 2 1 2 1 1 2 2 1 2 2 1 1 2 2 1 2 2 1 a a a a a b b a x a a a a b a a b x 记矩阵 21 22 11 12 a a a a 2 1 2 1 1 1 2 2 2 2 1 1 2 1 2 1 2 2 1 1 1 2 , , a b a b A b a b a A a a a a A 称 为一个二阶行列式,且 a a a a A a a a a det 1 1 2 2 1 2 2 1 2 1 2 2 1 1 1 2 A
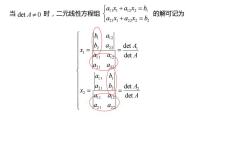
ax +a12X2 = b的解可记为当detA±0时,二元线性方程组[a21)+a22x2=b,ba2bdet A,a22xdet Aa12aa21b,aib2det A,a21X2det Aa2aila22a21
当 时,二元线性方程组 的解可记为 2 1 1 2 2 2 2 1 1 1 1 2 2 1 a x a x b a x a x b det A 0 A A a a a a a b a b x A A a a a a b a b a x det det det det 2 2 1 2 2 1 1 1 2 2 1 2 1 1 1 2 1 2 1 2 2 1 1 1 2 2 2 2 1 1 2 1

二阶行列式定义由四个数排成二行二列(横排称行、竖排称列)的数表aual2a21(22数[aia22 -a12a21称为数表所确定的二阶行列式,记为aii a2[a21 a22
由四个数排成二行二列(横排称行、竖排称列) 的数表 数 a a a a 11 22 12 21 称为数表所确定的 二阶行列式, 记为 11 12 21 22 a a a a 二阶行列式定义 11 12 21 22 a a a a

二阶行列式的计算一对角线法则a主对角线2=a1a22-(1221a21次对角线22
a21 11 a 12 a 22 a 主对角线 次对角线 对角线法则 11 22 a a . 12 21 a a 二阶行列式的计算

单选题1分设置99提交
1 - 99-77 ABCD 提交 单选题 1 分

+ai +a=b同理,对于三元线性方程组a21 +a222 +a23g =b2[a31+a2x2+a3g=b( b)bibraai2ar3aiiai3(anlai2a13ai2b2b2b2A =记矩阵A=A=a21A, =a22a21a22a23a23a21a22a23bs(b)b,a32(a31a33(asia32(as1a32a33a33)det A,x,det Adet Az当detA≠0时,三元线性方程组的解可记为X2det Adet A,X3det A
同理,对于三元线性方程组 3 1 1 3 2 2 3 3 3 3 2 1 1 2 2 2 2 3 3 2 1 1 1 1 2 2 1 3 3 1 a x a x a x b a x a x a x b a x a x a x b 记矩阵 3 1 3 2 3 2 1 2 2 2 1 1 1 2 1 3 3 1 3 3 3 2 1 2 2 3 1 1 1 1 3 2 3 3 2 3 3 2 2 2 2 3 1 1 2 1 3 1 3 1 3 2 3 3 2 1 2 2 2 3 1 1 1 2 1 3 , , , a a b a a b a a b A a b a a b a a b a A b a a b a a b a a A a a a a a a a a a A 当 det A 0 时,三元线性方程组的解可记为 A A x A A x A A x det det det det det det 3 3 2 2 1 1

ajiai2ai其中 det A=a21a22a23=a1a22a33+12a23a31+a132ia32a31a32a331322a31-a12a21a33-a11a23a32称为一个三阶行列式(1)对角线展开法展开式共6(3!)项每项是3个不同行不同列的元素乘积3项带正号(主对角线方向)、3项带负号(次对角线方向)
其中 1 3 2 2 3 1 1 2 2 1 3 3 1 1 2 3 3 2 1 1 2 2 3 3 1 2 2 3 3 1 1 3 2 1 3 2 3 1 3 2 3 3 2 1 2 2 2 3 1 1 1 2 1 3 det a a a a a a a a a a a a a a a a a a a a a a a a a a a A 称为一个三阶行列式. (1)对角线展开法 3 1 3 2 3 3 2 1 2 2 2 3 1 1 1 2 1 3 a a a a a a a a a • 展开式共 6(3!)项 • 每项是3个不同行不同列的元素乘积 • 3项带正号(主对角线方向)、3项带负号(次对角线方向)

aua12a13(2)按一行展开法a21a22a23aa7a21a22a23=aa20a33a31a33d32a1a32a31a32a33=aA, +ai2A2+ai3A3其中A1,A2,A3分别称为元素a1a12,a;的代数余子式aa21a12 =(-1)I+2 = (-1)+3Ai =(-1)I+Ia31a31a32a32a33a33
(2)按一行展开法 3 1 3 2 2 1 2 2 1 3 3 1 3 3 2 1 2 3 1 2 3 2 3 3 2 2 2 3 1 1 3 1 3 2 3 3 2 1 2 2 2 3 1 1 1 2 1 3 a a a a a a a a a a a a a a a a a a a a a a a a a1 1A1 1 a1 2A1 2 a1 3A1 3 其中 A11, A12, A13 分别称为元素 a11,a12,a13 的代数余子式 3 1 3 2 1 3 2 1 2 2 1 3 3 1 3 3 1 2 2 1 2 3 1 2 3 2 3 3 1 1 2 2 2 3 1 1 ( 1) , ( 1) , ( 1) a a a a A a a a a A a a a a A

定义ajana12a21a22a2n是由 A确定的一个数:设A是n阶方阵,n阶行列式detA=...:::anan2a(1)当n=1时,det A=ai|=au(2)当n≥2时,det A=auA+ai2A2+...+ainAn,其中A,=(-1)*iM,aiiainauj-1auj+1.:a2na21a2j-1a2j+1...·(j =1,2,...,n)M.:antannanj-1anj+1M,称为元素α,的余子式,A,称为元素a,的代数余子式上述归纳定义称为行列式按第1行展开
定义 设 A 是 n 阶方阵, n 阶行列式 det 是由 确定的一个数: 1 2 2 1 2 2 2 1 1 1 2 1 n n n n n n a a a a a a a a a A A (1)当 n 1 时, det A a11 a11 (2)当 n 2 时 , det A a1 1A1 1 a1 2A1 2 a1n A1n ,其中 j j A j M1 1 1 ( 1) n n j n j n n j j n j j n j a a a a a a a a a a a a M 1 1 1 2 1 2 1 2 1 2 1 1 1 1 1 1 1 1 ( j 1,2, ,n) M1 j 称为元素 a1 j 的余子式, A1 j 称为元素 a1 j 的代数余子式。 上述归纳定义称为行列式按第1行展开
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《线性代数》课程教学资源(讲稿B,高教版)第三章 n维向量空间 3-1 n维向量空间的概念.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第一章 矩阵及其初等变换 1-4 分块矩阵.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第一章 矩阵及其初等变换 1-3 逆矩阵.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第一章 矩阵及其初等变换 1-2 高斯消元法和矩阵的初等变换.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第一章 矩阵及其初等变换 1-1 矩阵及其运算.pdf
- 《高等数学》课程教学资源(课件讲稿)第1章 第1讲 函数.pdf
- 《线性代数》课程教学资源(章节讲稿,C)3-4 线性方程组解的结构新.pdf
- 《线性代数》课程教学资源(章节讲稿,C)3-3 向量组的秩与极大无关组.pdf
- 《线性代数》课程教学资源(章节讲稿,C)3-2 向量组的线性相关性.pdf
- 《线性代数》课程教学资源(章节讲稿,C)3-1 n维向量空间的概念.pdf
- 《线性代数》课程教学资源(章节讲稿,C)2-5 矩阵的秩.pdf
- 《线性代数》课程教学资源(章节讲稿,C)2-4 克拉默法则.pdf
- 《线性代数》课程教学资源(章节讲稿,C)2-3 拉普拉斯定理.pdf
- 《线性代数》课程教学资源(章节讲稿,C)2-2 n阶行列式的性质与计算.pdf
- 《线性代数》课程教学资源(章节讲稿,C)2-1 n阶行列式的定义.pdf
- 《线性代数》课程教学资源(章节讲稿,C)1-4 分块矩阵.pdf
- 《线性代数》课程教学资源(章节讲稿,C)1-3 逆矩阵.pdf
- 《线性代数》课程教学资源(章节讲稿,C)1-2 高斯消元法和矩阵的初等变换.pdf
- 《线性代数》课程教学资源(章节讲稿,C)1-1 矩阵及其运算.pdf
- 《高等数学》课程教学资源(课件讲稿)第3章 第3讲 泰勒中值定理.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第二章 行列式 2-2 n阶行列式的性质与计算.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第二章 行列式 2-3 拉普拉斯定理.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第二章 行列式 2-4 克拉默法则.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第二章 行列式 2-5 矩阵的秩.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第三章 n维向量空间 3-2 向量组的线性相关性.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第三章 n维向量空间 3-3 向量组的秩与极大无关组.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第三章 n维向量空间 3-4 线性方程组解的结构.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第四章 特征值与特征向量 4-1 特征值与特征向量的概念与计算.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第四章 特征值与特征向量 4-2 矩阵的相似对角化.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第四章 特征值与特征向量 4-3 n维向量空间的正交性.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第四章 特征值与特征向量 4-4实对称矩阵的相似对角化.pdf
- 《高等数学》课程教学资源(课件讲稿)第1章——第1节映射与函数.pdf
- 《高等数学》课程教学资源(课件讲稿)第1章——第2节数列的极限.pdf
- 《高等数学》课程教学资源(课件讲稿)第1章——第10节闭区间上连续函数的性质.pdf
- 《高等数学》课程教学资源(课件讲稿)第1章——第3节函数的极限.pdf
- 《高等数学》课程教学资源(课件讲稿)第1章——第4节无穷小与无穷大.pdf
- 《高等数学》课程教学资源(课件讲稿)第1章——第5节极限运算法则.pdf
- 《高等数学》课程教学资源(课件讲稿)第1章——第6节极限存在准则 两个重要极限.pdf
- 《高等数学》课程教学资源(课件讲稿)第1章——第7节无穷小的比较.pdf
- 《高等数学》课程教学资源(课件讲稿)第1章——第8节函数的连续性与间断点.pdf
