《线性代数》课程教学资源(讲稿B,高教版)第三章 n维向量空间 3-1 n维向量空间的概念

第三章n维向量空间3-1 n维向量空间的概念3-2向量组的线性相关性3-3向量组的秩与极大无关组3-4 线性方程组解的结构
第三章 n 维向量空间 3-1 n 维向量空间的概念 3-2 向量组的线性相关性 3-3 向量组的秩与极大无关组 3-4 线性方程组解的结构

3-1n维向量空间的概念引入Op=(a,a2,a,)1°空间直角坐标系中,向径OP是一个三维向量,坐标表示为0203(o203),2°矩阵14的每一行元素可以构成一个行矩阵-30(14),0-3(000102)12030每一列元素可以构成一个列矩阵4-3010203°n元线性方程ax+azx2+...+a,x=b的系数可以记为(ai,a,"",an)
3-1 n 维向量空间的概念 OP 引入 1°空间直角坐标系中,向径 是一个三维向量,坐标表示为 ( , , ) OP a1 a2 a3 2°矩阵 的每一行元素可以构成一个行矩阵 0 1 0 2 1 3 0 4 0 2 0 3 0 1 0 2 , 1 3 0 4 , 0 2 0 3 , 每一列元素可以构成一个列矩阵 2 4 3 , 0 0 0 , 1 3 2 , 0 1 0 3° n 元线性方程 a1 x1 a2 x2 an xn b 的系数可以记为 ( , , , ) a1 a2 an

一、向量及向量空间定义1数域P上的n个数组成的有序数组α=(a,αz,,a,)称为一个n维向量。ai注a2列向量:(1)行向量:(ai,a2,.,an)an)(2)a,称为向量的分量(i=1,2,,n)(3)设向量α=(a,a2,,a,),β=(b,bz,,b,),若a,=b,(i=1,2,,n),则称向量相等:α=β0 =(0,0,.,0)(4)零向量(5)负向量-α=(aj,-a2,,-an)
定义1 数域 P上的 n 个数组成的有序数组 (a1 ,a2 , ,an ) 称为一个 n 维向量。 ( , , , ) (1)行向量: a1 a2 an 列向量: n a a a 2 1 a (i 1,2, ,n) (2) i 称为向量的分量 (3)设向量 ,若 ,则称 向量相等: ( , , , ), ( , , , ) a1 a2 an b1 b2 bn a b (i 1,2, ,n) i i 注 (4)零向量 ( , , , ) a1 a2 an 0 (0,0, ,0) (5)负向量 一、向量及向量空间

定义2(向量的线性运算)设向量α=(aj,az,.",a,),β=(b,bz,".,b,),keP(数域)向量加法α+β=(a, +br,a2 +bz,"",an +bn)数乘向量ka =(ka,kaz,...,kan)定义3(n维实向量空间Rn)全体n维向量的集合,对于加法和数乘运算封闭,且满足下列运算规律(1) α+β=β+α;(5) 1α =α;(2) (α +β)+=α+(β+);(6) k(lα) =(kl)α;(3) α+0=α;(7) k(α +β)=kα+kβ:(4) α+(-α)=0,(8) (k+I)α = kα+lα
定义2 (向量的线性运算) 设向量 (a1 ,a2 , ,an ), (b1 ,b2 , ,bn ), k P (数域) 向量加法 数乘向量 ( , , , ) a1 b1 a2 b2 an bn ( , , , ) 1 2 n k ka ka ka 定义3 ( n 维实向量空间 Rn) 全体 n 维向量的集合,对于加法和数乘运算封闭,且满足下列运算规律: (4) ( ) 0; (3) 0 ; (2) ( ) ( ); (1) ; (8) ( ) . (7) ( ) ; (6) ( ) ( ) ; (5) 1 ; k l k l k k k k l k l

ax +ai2x2+...+ainx,=ba21X, +a22X2 +..+a2nx, =b,例如,n元线性方程组可记为向量方程:+am2X2+...+amx,=bmL(b)ay2b2a22d21aanXa+x2+..+x=b+X2Xb.amlCX2X =或 Xa +x22 +.+x,α, =(α1,α2,*,αn)X=b(解向量)x
例如,n 元线性方程组 可记为向量方程: m m mn n m n n n n a x a x a x b a x a x a x b a x a x a x b 1 1 2 2 2 1 1 2 2 2 2 2 1 1 1 1 2 2 1 1 mn m n n n m m b b b a a a x a a a x a a a x 2 1 2 1 2 2 2 1 2 2 1 2 1 1 1 1 x1 1 x2 2 xn n b 或 x1 1 x2 2 xn n (1 ,2 , ,n )X b n x x x X 2 1 (解向量)

二、向量空间与子空间1.定义设V是n维向量的集合,如果V非空且对向量的两种运算封闭,即V满足:(1)有α+βeVVα,BeV,有kαeV(2)VαeV,kER,则称V是一个向量空间
1.定义 设V是n维向量的集合,如果V非空,且对向量 的两种运算封闭,即 V 满足: (1) , V, 有 + V (2) V ,k R, 有 k V 则称 V 是一个向量空间. 二、向量空间与子空间

例如(1)全体 n维向量构成一个向量空间,称为 n维向量空间:记作R"(2) Vi ={(0, a2, ... , an) / a; E R, i= 2, 3, ... n) 是一个向量空间,且V,CR",称为R"的一个子空间(3)集合V,=(x=(1,x2,……,x,E R)不是向量空间.因为若α= (1,a2...,a,)e V2,则2α =(2,2a2...., 2a,) V2
例如 (2) V1 = { ( 0, a2 , . , an ) | ai R, i = 2, 3, . n } 是一 个向量空间,且V1 R n,称为 R n 的一个子空间. (1) 全体 n 维向量构成一个向量空间,称为 n 维 向量空间:记作 R n . 2 2 2 2 2 2 (3) { (1, , , } (1, , , ) , 2 (2,2 , ,2 ) . n n n V x x x R a a V a a V 集合 不是向量空间.因为 若 则

子空间定义4(R"的子空间)非空向量集合VR",如果V对于R"的线性运算也构成一个向量空间,则称V为R"的一个子空间。定理1非空子集V是R"的子空间一V对于加法和数乘运算封闭例1在3维向量空间R3中,定义两个子集:V=((x,x2,x)x +x2 +x =0)是R的子空间V2 =((Xi,X2,x) X +x2 +x =1)不是R的子空间
定义4 ( Rn 的子空间) 子空间 非空向量集合 ,如果 对于 的线性运算也构成一个向量空间,则 称 为 的一个子空间。 3 R n V R n V R 定理1 非空子集 是 的子空间 对于加法和数乘运算封闭 n V R V 例1 在3维向量空间 中,定义两个子集: n V R {( , , ) 1} {( , , ) 0} 2 1 2 3 1 2 3 1 1 2 3 1 2 3 V x x x x x x V x x x x x x 是 R 3 的子空间 不是 R 3 的子空间

单选题设置1分V=((x1,×2×3)|x3=0是R3的子空间对错提交
𝑉3 = { (𝑥1, 𝑥2, 𝑥3) ห 𝑥3 = 0 }是𝑅 3的子空间 对 错 A B 提交 单选题 1分
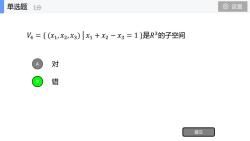
单选题设置1分V4=(×1,X2,X3)1+×2—X=1}是R3的子空间对错提交
𝑉4 = { (𝑥1, 𝑥2, 𝑥3) ห 𝑥1 + 𝑥2 − 𝑥3 = 1 }是𝑅 3的子空间 对 错 A B 提交 单选题 1分
按次数下载不扣除下载券;
注册用户24小时内重复下载只扣除一次;
顺序:VIP每日次数-->可用次数-->下载券;
- 《线性代数》课程教学资源(讲稿B,高教版)第一章 矩阵及其初等变换 1-4 分块矩阵.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第一章 矩阵及其初等变换 1-3 逆矩阵.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第一章 矩阵及其初等变换 1-2 高斯消元法和矩阵的初等变换.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第一章 矩阵及其初等变换 1-1 矩阵及其运算.pdf
- 《高等数学》课程教学资源(课件讲稿)第1章 第1讲 函数.pdf
- 《线性代数》课程教学资源(章节讲稿,C)3-4 线性方程组解的结构新.pdf
- 《线性代数》课程教学资源(章节讲稿,C)3-3 向量组的秩与极大无关组.pdf
- 《线性代数》课程教学资源(章节讲稿,C)3-2 向量组的线性相关性.pdf
- 《线性代数》课程教学资源(章节讲稿,C)3-1 n维向量空间的概念.pdf
- 《线性代数》课程教学资源(章节讲稿,C)2-5 矩阵的秩.pdf
- 《线性代数》课程教学资源(章节讲稿,C)2-4 克拉默法则.pdf
- 《线性代数》课程教学资源(章节讲稿,C)2-3 拉普拉斯定理.pdf
- 《线性代数》课程教学资源(章节讲稿,C)2-2 n阶行列式的性质与计算.pdf
- 《线性代数》课程教学资源(章节讲稿,C)2-1 n阶行列式的定义.pdf
- 《线性代数》课程教学资源(章节讲稿,C)1-4 分块矩阵.pdf
- 《线性代数》课程教学资源(章节讲稿,C)1-3 逆矩阵.pdf
- 《线性代数》课程教学资源(章节讲稿,C)1-2 高斯消元法和矩阵的初等变换.pdf
- 《线性代数》课程教学资源(章节讲稿,C)1-1 矩阵及其运算.pdf
- 《高等数学》课程教学资源(课件讲稿)第3章 第3讲 泰勒中值定理.pdf
- 《高等数学》课程教学资源(课件讲稿)第3章 第3讲 泰勒中值定理.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第二章 行列式 2-1 n阶行列式的定义.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第二章 行列式 2-2 n阶行列式的性质与计算.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第二章 行列式 2-3 拉普拉斯定理.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第二章 行列式 2-4 克拉默法则.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第二章 行列式 2-5 矩阵的秩.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第三章 n维向量空间 3-2 向量组的线性相关性.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第三章 n维向量空间 3-3 向量组的秩与极大无关组.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第三章 n维向量空间 3-4 线性方程组解的结构.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第四章 特征值与特征向量 4-1 特征值与特征向量的概念与计算.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第四章 特征值与特征向量 4-2 矩阵的相似对角化.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第四章 特征值与特征向量 4-3 n维向量空间的正交性.pdf
- 《线性代数》课程教学资源(讲稿B,高教版)第四章 特征值与特征向量 4-4实对称矩阵的相似对角化.pdf
- 《高等数学》课程教学资源(课件讲稿)第1章——第1节映射与函数.pdf
- 《高等数学》课程教学资源(课件讲稿)第1章——第2节数列的极限.pdf
- 《高等数学》课程教学资源(课件讲稿)第1章——第10节闭区间上连续函数的性质.pdf
- 《高等数学》课程教学资源(课件讲稿)第1章——第3节函数的极限.pdf
- 《高等数学》课程教学资源(课件讲稿)第1章——第4节无穷小与无穷大.pdf
- 《高等数学》课程教学资源(课件讲稿)第1章——第5节极限运算法则.pdf
- 《高等数学》课程教学资源(课件讲稿)第1章——第6节极限存在准则 两个重要极限.pdf
- 《高等数学》课程教学资源(课件讲稿)第1章——第7节无穷小的比较.pdf
