《线性代数》课程教学资源（讲稿B，高教版）第三章 n维向量空间 3-3 向量组的秩与极大无关组

3-3向量组的秩与极大无关组引例0120,α4 =找出向量组α, =中所有线性无关的部分组。,α2α3-02-10011111行变换R(A) = 2210011-1作矩阵 A=1000001-12含1个向量的线性无关组：α%；α2Qg;α4含2个向量的线性无关组：αααααα4α2,α；α2α4；αα4含3个向量的部分组：α,α2,α，α1,α2,α4，α2α3α都线性相关,α2,α,α4也线性相关

3-3 向量组的秩与极大无关组 引例                                              0 2 1 , 2 0 1 , 1 1 0 , 1 1 1 找出向量组 1 2 3 4 中所有线性无关的部分组。 作矩阵             0 2 1 2 0 1 1 1 0 1 1 1 A             0 1 1 0 1 1 0 1 0 0 0 1 行变换 R(A)  2 含1个向量的线性无关组： 1 2 3 4  ;  ;  ;  含2个向量的线性无关组： 𝛼1, 𝛼2; 𝛼1, 𝛼3; 𝛼1,𝛼4；𝛼2, 𝛼3；𝛼2, 𝛼4；𝛼3, 𝛼4 含3个向量的部分组： 𝛼1, 𝛼2, 𝛼3， 𝛼1, 𝛼2, 𝛼4， 𝛼2, 𝛼3, 𝛼4 都线性相关， 也线性相关。 𝛼1, 𝛼2, 𝛼3, 𝛼4

思考（1）线性无关的部分组所含向量个数是否存在最大值？（此例中，最大值为2）（2）最大规模的部分线性无关组是否唯一？（此例中，不唯一）（3）找出一个最大规模的部分线性无关组α1,α2，其它向量能否由它线性表示？β1,β2,β3,βai,a2,α,α01101β=β-β2,β4=β+β20A=01-1112→α=α-, α=α +α,00000-12可以由它线性表示，且表示法唯一

思考 （1）线性无关的部分组所含向量个数是否存在最大值？ （此例中，最大值为2） （2）最大规模的部分线性无关组是否唯一？ （此例中，不唯一） （3）找出一个最大规模的部分线性无关组 1 ,2 ，其它向量能否由它线性表示？             0 1 1 0 1 1 0 1 0 0 0 1             0 2 1 2 0 1 1 1 0 1 1 1 A 1 2 3 4  , , , 1 2 3 4  ,  ,  ,  3  1  2 ，4  1  2 3 1 2 ，4 1 2 可以由它线性表示，且表示法唯一

一、向量组的秩与极大无关组定义若向量组T满足：（1）在T中有r个向量αi,α2,,α，线性无关；（2）T中任意r+1个向量（如果有）都线性相关。则称αi,α2，,α,是向量组T的一个极大线性无关组（简称极大无关组），数r称为向量组的秩注1°极大无关组一般不唯一。但所含向量的个数是固定的，即为向量组的秩2°只含零向量的向量组秩为0，不存在极大无关组。3°线性无关的向量组αi,α2，,α，，本身即是极大无关组，秩为s

一、向量组的秩与极大无关组 定义 若向量组 T 满足： （1）在 T 中有 r 个向量 线性无关 ;   r , , , 1 2  （2）T 中任意 r+1 个向量（如果有）都线性相关 。 则称 是向量组 T 的一个极大线性无关组（简称极大无关组），数 r 称为向量组的秩。   r , , , 1 2  注 1°极大无关组一般不唯一。但所含向量的个数是固定的，即为向量组的秩。 2°只含零向量的向量组秩为0，不存在极大无关组。 3°线性无关的向量组 1 ,2 ,  ,s ，本身即是极大无关组，秩为 s

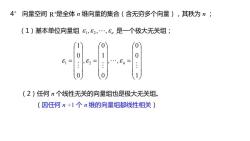
4°向量空间R"是全体n维向量的集合（含无穷多个向量），其秩为n（1）基本单位向量组81,&2，,8n是一个极大无关组；000100（2）任何n个线性无关的向量组也是极大无关组。（因任何n+1个n维的向量组都线性相关）

4° 向量空间 R n 是全体 n 维向量的集合（含无穷多个向量），其秩为 n ； n  ,  , ,  1 2  （2）任何 n 个线性无关的向量组也是极大无关组。 （因任何 n +1 个 n 维的向量组都线性相关）                                              1 0 0 , , 0 1 0 , 0 0 1 1 2     n    （1）基本单位向量组 是一个极大无关组；

向量组线性无关台向量组的秩=向量组所含向量个数向量组线性相关台向量组的秩<向量组所含向量个数思考：矩阵的秩与向量组的秩有何联系？能否利用矩阵的初等变换求解向量组的极大无关组？加油！

向量组线性无关 向量组的秩 = 向量组所含向量个数. 向量组线性相关 向量组的秩 < 向量组所含向量个数. 思考：矩阵的秩与向量组的秩有何联系？能否利用矩阵的初 等变换求解向量组的极大无关组？

行初等变换→B,若A定理1则A的任意k个(1≤k≤n)个列向量与B的对应k个列向量有相同的线性相关性行初等变换证>BkA任取A的k个列向量所得AkX=0与BkX=0同时有非零解或只有零解A,的列向量与B,的列向量有相同的线性相关性加油！

B 的对应 k 个列向量有相同的线性相关性. 定理1 若 证 任取A的k个列向量所得 Ak X = 0 与 Bk X = 0 同时有非零解或只有零解. Ak 的列向量与 Bk 的列向量有相同的线性相关性. , A B m n  行初等变换 , A B k k  行初等变换 则A的任意 k个( 1≤ k ≤ n)个列向量与

结论1：行（列）初等变换不改变矩阵列（行）向量间的线性关系30112-1例设矩阵A=050246列向量αi,αz,α3,α,间有线性关系α=α,+2α,-α加油！

结论1：行（列）初等变换不改变矩阵列（行）向量间的线性关系. 1 1 3 0 0 2 1 5 6 0 2 4 例 设矩阵A             1 2 3 4 4 1 2 3 , 2            列向量 间有线性关系

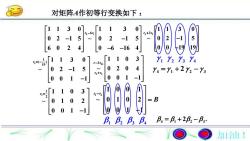
对矩阵A作初等行变换如下：3031I31+3r250511916-16431 2 3 4031940514 = X1 +2 2 -3?01202=B20-2福001β, =β, +2β, -β3β β, β, β加油！

对矩阵A作初等行变换如下 ： 3 1 6 1 1 3 0 1 1 3 0 0 2 1 5 ~ 0 2 1 5 6 0 2 4 0 6 16 4 r r                          3 2 3 1 1 3 0 ~ 0 2 1 5 0 0 19 19 r r              3 1 ( ) 19 1 1 3 0 ~ 0 2 1 5 0 0 1 1 r               31 2 3 3 1 1 0 3 ~ 0 2 0 4 0 0 1 1 r r r r              1 2 3 4     2 1 2 1 1 0 3 ~ 0 1 0 2 0 0 1 1 r             1 2 1 0 0 1 ~ 0 1 0 2 0 0 1 1 r r B                  1 2 3 4 4 1 2 3        2 . 4 1 2 3        2

矩阵A的列秩：A的列向量组的秩：矩阵A的行秩：A的行向量组的秩结论2：初等行(列)变换不改变矩阵的列(行)秩加油！

矩阵A的列秩：A的列向量组的秩； 矩阵A的行秩：A的行向量组的秩. 结论2：初等行(列)变换不改变矩阵的列(行)秩

定理2矩阵的行秩=列秩=矩阵的秩证 设 R(A) = r， A=行初等变换>B(行阶梯形矩阵),B有r个非零行，B的r个非零行的非零首元素所在的r个列向量线性无关，为B的列向量组的极大无关组加油！

定理2 矩阵的行秩 = 列秩 = 矩阵的秩. 证 设 R(A) = r, A B  ( ), 行初等变换 行阶梯形矩阵 B有 r 个非零行，B的r 个非零行的非零首元素 所在的r 个列向量线性无关，为B的列向量组的 极大无关组