《高等数学》课程教学资源（课件讲稿）第四章课件_第一节不定积分

第四章 不定积分 微分法：x)=(?) 互逆运算 积分法：(？)=f(x)

第四章 微分法: 积分法: 互逆运算 不定积分

第一节 第四章 不定积分的桡念与性质 一、原函数与不定积分的概念 二、基本积分表 三、不定积分的性质 HIGH EDUCATION PRESS

二、 基本积分表 三、不定积分的性质 一、 原函数与不定积分的概念 第一节 机动 目录 上页 下页 返回 结束 不定积分的概念与性质 第四章

一、 原函数与不定积分的概念 引例：一个质量为m的质点，在变力F=Asint的作 下沿直线运动，试求质点的运动速度v(t) 根据牛顷第二定律，加速度a)=-4m, mm 因此间题转化为：已知v0=sn,求W=? m 定义1.若在区间I上定义的两个函数F(x)及f 满F4x)=f(x)或dF(x)=f(x)dr,则称F(x)为f 在区间I上的一个原函数 (x) 如引例中，二sint的原函数有 -coS t. cost+3.L m m HIGH EDUCATION PRESS

一、 原函数与不定积分的概念 引例: 一个质量为 m 的质点, 下沿直线运动 , 因此问题转化为: 已知 求 在变力 试求质点的运动速度 机动 目录 上页 下页 返回 结束 根据牛顿第二定律, 加速度 定义 1 . 若在区间 I 上定义的两个函数 F (x) 及 f 满足(x) 在区间 I 上的一个原函数 . 则称 F (x) 为f (x) 如引例中, 的原函数有

问题： 1.在什么条件下，一个函数的原函数存在？ 2.若原函数存在，它如何表示？ 定理1.若函数f(x)在区间I上连续，则f(x)在I上 存在原函数. (下章证明) 初等函数在定义区间上连续 初等函数在定义区间上有原函数 HIGH EDUCATION PRESS 机动 结球

问题: 1. 在什么条件下, 一个函数的原函数存在 ? 2. 若原函数存在, 它如何表示 ? 定理1. 存在原函数 . (下章证明) 初等函数在定义区间上连续 初等函数在定义区间上有原函数 机动 目录 上页 下页 返回 结束

定理2.若F(x)是f(x)的一个原函数，则f(x)的所有 原函数都在函数族F(x)+C(C为任意常数)内 证：1)Q(F(x)+C)=F4x)=f(x) 1F(x)+C是f(x)的原函数 2)设F(x)是f(x)的任一原函数，即 F dx)=f(x) 又知 Fdx)=f(x) [F(x)-F(x)]=F4x)-F4x)=f(x)-f(x)=0 故 F(x)=F(x)+C。(C0为某个常数) 即F(x)=F(x)+C。属于函数族F(x)+C HIGH EDUCATION PRESS 结

定理 2. 原函数都在函数族 ( C 为任意常数 ) 内 证 . : 1) 又知 故 即 属于函数族 机动 目录 上页 下页 返回 结束 即

定义2.f(x)在区间I上的原函数全体称为f(x)在I 上的不定积分，记作Of(x)dx,其中 0- 积分号 f(x)一被积函数； (P183) x;积分变量； f(x)dc一被积表达式： 若Fx)=f(x),则 òf(x)dx=F(x)+C(C为任意常数) 例如， Ce*dx ex+C C称为积分常数 02dx=}x3+C 不可丢！ (sin xdx cosx+C HIGH EDUCATION PRESS 结束

定义 2. 在区间 I 上的原函数全体称为 上的不定积分, 其中 — 积分号 ; — 被积函数; — 积分变量; — 被积表达式. (P183) 若 则 ( C 为任意常数 ) C 称为积分常数 不可丢 ! 例如, 记作 机动 目录 上页 下页 返回 结束

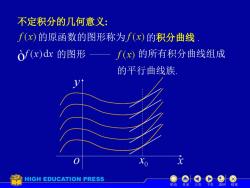
不定积分的几何意义： f(x)的原函数的图形称为f(x)的积分曲线 òf(x)d的图形 —f(x)的所有积分曲线组成 的平行曲线族 Xo HIGH EDUCATION PRESS 目录 返回 结球

不定积分的几何意义: 的原函数的图形称为 的图形 的所有积分曲线组成 的平行曲线族. 机动 目录 上页 下页 返回 结束 的积分曲线

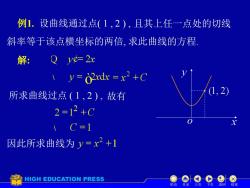
例1.设曲线通过点(1,2)，且其上任一点处的切线 斜率等于该点横坐标的两倍，求此曲线的方程 解：Qye=2x =xdx =x2+C 所求曲线过点(1,2)，故有 1,2) 2=12+C 因此所求曲线为y=x2+1 HIGH EDUCATION PRESS 目录 结球

例1. 设曲线通过点( 1 , 2 ) , 且其上任一点处的切线 斜率等于该点横坐标的两倍, 求此曲线的方程. 解: 所求曲线过点 ( 1 , 2 ) , 故有 因此所求曲线为 机动 目录 上页 下页 返回 结束

例2.质点在距地面xo处以初速y。垂直上抛，不计阻 力，求它的运动规律 解：取质点运动轨迹为坐标轴，原点在地面，指向朝上 质点抛出时刻为t=0。此时质点位置为x,初速为vo 设时刻t质点所在位置为x=x(t),则 dx =v(t (运动速度) dt x=x(t) 再由此求x(t) d2x dv ·x0=x(0) dt =-9 (加速度) 先由此求v(t) HIGH EDUCATION PRESS 凯动 结

例2. 质点在距地面 处以初速 力, 求它的运动规律. 解: 取质点运动轨迹为坐标轴, 原点在地面, 指向朝上 质点抛出时刻为 , 此时质点位置为 初速为 设时刻 t 质点所在位置为 则 (运动速度) (加速度) 机动 目录 上页 下页 返回 结束 垂直上抛 , 不计阻 先由此求 再由此求

先求v():由 dy=-g知 v()=d-g)dt=-gt+Cl x=x(t) 由v(0)=%,得C1=Vo,故 ·x0=x(0) v(t)=gt+vo 再求x0).由 dx=-gy+o,知 m x(t)=d-gr +vo)dt =-79r2+vol+C2 由x(0)=x,得C2=x0,于是所求运动规律为 x()=-2g+vo1+x0 HIGH EDUCATION PRESS 结球

先求 由 知 再求 于是所求运动规律为 由 知 机动 目录 上页 下页 返回 结束 故