《高等数学》课程教学资源（PPT课件）Ⅱ_第八章第一节 向量及其线性运算

高等数学（下册） 主讲：卢刚夫

高等数学（下册） 主讲：卢刚夫

高等数学（下册） 的主要内容（红色章节） 1.分析基础：函数，极限，连续止册第1) 2.微积分学：一元微积分让册第2、3、4、5、6章) 多元微积分（下期9,10,1） 3.微分方程上册第7章) 4.无穷级数（下册12） 5.向量代数与空间解析几何（下册第8）

1. 分析基础: 函数 , 极限, 连续 (上册 第1章) 2. 微积分学: 一元微积分(上册 第2、3、4、5、6章) 5. 向量代数与空间解析几何(下册第8章) 4. 无穷级数(下册12章) 3. 微分方程(上册 第7章) 高等数学（下册）的主要内容（红色章节） 多元微积分(下册9,10，11章)

第、章 向量代数与空间解析几何 第一部分向量代数 第二部分空间解析几何 在三维空间中： 空间形式一 点，线，面 lt 数量关系 坐标，方程（组) 基本方法 坐标法：向量法

数量关系 — 第八章 第一部分 向量代数 第二部分 空间解析几何 在三维空间中: 空间形式 — 点, 线, 面 基本方法 — 坐标法; 向量法 坐标, 方程（组） 向量代数与空间解析几何

第一节 第七章 句量及其线性运算 向量的概念 二、 向量的线性运算 三、空间直角坐标系 四、利用坐标作向量的线性运算 五、向量的模、方向角、投影

四、利用坐标作向量的线性运算 第一节 一、向量的概念 二、向量的线性运算 三、空间直角坐标系 五、向量的模、方向角、投影 机动 目录 上页 下页 返回 结束 向量及其线性运算 第七章

一、向量的概念 向量：既有大小，又有方向的量称为向量（又称矢量） 表示法有向线段M2,或a,或a. 向量的模：向量的大小，记作MM2,或，或a: 向径（矢径）：起点为原点的向量 自由向量：与起点无关的向量 单位向量：模为1的向量，记作°或a°. 零向量：模为0的向量，记作0，或0. 下页返回结束

表示法: 向量的模 : 向量的大小, 一、向量的概念 向量: (又称矢量). M1 M 2 既有大小, 又有方向的量称为向量 向径 (矢径): 自由向量: 与起点无关的向量. 起点为原点的向量. 单位向量: 模为 1 的向量, 零向量: 模为 0 的向量, 有向线段 M1 M2 , 或 a , 机动 目录 上页 下页 返回 结束a

若向量ā与b大小相等，方向相同，则称a与b相等 记作a=b; 若向量a与b方向相同或相反，则称ā与平行，记作 a/b,规定：零向量与任何向量平行； 与ā的模相同，但方向相反的向量称为a的负向量， 记作-a; 因平行向量可平移到同一直线上，故两向量平行又称 两向量共线 若k(C3)个向量经平移可移到同一平面上，则称此k 个向量共面

规定: 零向量与任何向量平行 ; 若向量 a 与 b大小相等, 方向相同, 则称 a 与 b 相等, 记作 a＝b ; 若向量 a 与 b 方向相同或相反, 则称 a 与 b 平行, a∥b ; 与 a 的模相同, 但方向相反的向量称为 a 的负向量, 记作 因平行向量可平移到同一直线上, 故两向量平行又称 两向量共线 . 若 k (≥3)个向量经平移可移到同一平面上 , 则称此 k 个向量共面 . 记作－a ; 机动 目录 上页 下页 返回 结束

二、向量的线性运算 1.向量的加法 平行四边形法则： (a+B)+c b+c a+(+c) a:b 三角形法则： a+b a 运算规律：交换律a+b=b+a 结合律(a+b)+c=a+(b+e)=a+b+ 三角形法则可推广到多个向量相加 上页下页返回结束

二、向量的线性运算 1. 向量的加法 三角形法则: 平行四边形法则: 运算规律 : 交换律 结合律 三角形法则可推广到多个向量相加 . 机动 目录 上页 下页 返回 结束 b b a + b = b + a ( a + b ) + c = a + ( b + c ) = a + b + c a b c a + b b + c a + ( b + c ) ( a + b ) + c a a a + b a + b

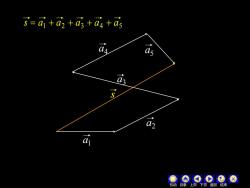
s=a+a2+d3+a4+a5 as a a 返回 结

机动 目录 上页 下页 返回 结束 s a3 a4 5 a a2 a1 1 2 3 4 5 s = a + a + a + a + a

2.向量的减法 b-a-b+(-a) 特别当b=a时，有 b a-a=a+(-a=0 三角不等式 a+b s a+b a-b s a+b 上页下页返回结束

2. 向量的减法 三角不等式 机动 目录 上页 下页 返回 结束 a

3.向量与数的乘法 入是一个数，入与d的乘积是一个新向量，记作入ā. 规定：2>0时，a与a同向，a=2a; 2<0时，2a与a反向，a=-a; 2=0时，2a=0. 可见 总之 Aa =aa la=a; 运算律：结合律2(ud)=u(2ad)=九ua-1a=-a, 分配律(+四)a=九a+ud (a+b)=2a+b 若a#0,则h单位向量d-a 因此a=aa P08

a a    =  3. 向量与数的乘法  是一个数 , a .   规定 : 1a a ;   = 可见 1a a ;   − = −  与 a 的乘积是一个新向量, 记作 总之: 运算律 : 结合律 ( a)    ( a)  =   a  =   分配律 (a b)    + a b   =  +  =  则有单位向量 a . 1 a a   因此    a = a a 机动 目录 上页 下页 返回 结束