《高等数学》课程教学资源（PPT课件）Ⅱ_第八章第六节 空间曲线及其方程

第之节 第七章 空间曲我线及其方程 空间曲线的一般方程 二、空间曲线的参数方程 三、空间曲线在坐标面上的投影

第七章 一、空间曲线的一般方程 二、空间曲线的参数方程 三、空间曲线在坐标面上的投影 第六节 机动 目录 上页 下页 返回 结束 空间曲线及其方程

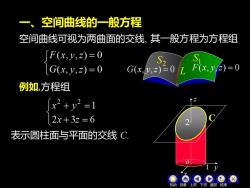
一、空间曲线的一般方程 空间曲线可视为两曲面的交线，其一般方程为方程组 F(x,y,z)=0 S2 G(x,y,z)=0 G(x,y,)=( (x,y,E)=0 例如，方程组 x2+y2=1 2x+3z=6 表示圆柱面与平面的交线 C 上页 下页返回结束

一、空间曲线的一般方程 空间曲线可视为两曲面的交线, 其一般方程为方程组 S2 L G(x, y,z) = 0 F(x, y,z) = 0 1 S 例如,方程组 表示圆柱面与平面的交线 C. x z 1 y o C 2 机动 目录 上页 下页 返回 结束

又如，方程组 2=a2-x2 x2+y2-ax=0 表示上半球面与圆柱面的交线C, Q

又如,方程组 表示上半球面与圆柱面的交线C. y x z a 机动 目录 上页 下页 返回 结束

二、空间曲线的参数方程 将曲线C上的动点坐标x,y表示成参数t的函数： (x=x(t) 称它为空间曲线的 y=y(t) 参数方程 2=z(t) 例如圆柱螺旋线的参数方程为 (详见下页) x=acosot 1 y=asinot 令0=0t,b= x=acos z =vt y=asin z=b0 当0=2π时，上升高度h=2πb,称为螺距 下页返回结束

z x y o 二、空间曲线的参数方程 将曲线C上的动点坐标x, y, z表示成参数t 的函数: 称它为空间曲线的 参数方程. 例如,圆柱螺旋线    v 令 = t , b = h = 2 b 的参数方程为 （详见下页） 上升高度 , 称为螺距 .  M 机动 目录 上页 下页 返回 结束

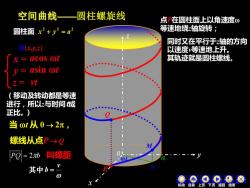
空间曲线 圆柱螺旋线 点P在圆柱面上以角速度0 圆柱面x2+y2=a 等速地绕轴旋转； 同时又在平行于轴的方向 (x.V) 以速度等速地上升。 acos ot 其轨迹就是圆柱螺线。 y asin ot 乙= （移动及转动都是等速 进行，所以z与时间城 正比。) 当ot从0→2元， 螺线从点P→Q PO=2劢叫螺距 其中b= 0 机动 下页返回结束

空间曲线——圆柱螺旋线 P 同时又在平行于z轴的方向 以速度v等速地上升。 其轨迹就是圆柱螺线。 圆柱面 2 2 2 x + y = a y z 0 x a x = y = z = acos t vt M(x,y,z) asin t t M 螺线从点P → Q 当 t 从 0 → 2， PQ = 2b 叫螺距 N . Q （移动及转动都是等速 进行，所以z与时间t成 正比。) 点P在圆柱面上以角速度 等速地绕z轴旋转；  v 其中 b = 机动 目录 上页 下页 返回 结束

螺旋线的参数方程还可以写为 x acos0 y=asine (8=am、b=0 z=b0 螺旋线的重要性质： 上升的高度与转过的角度成正比. 即 3: b0→b8+bC, C=2时上升的高度 h=2b元 螺距 上页下页返回结束

螺旋线的参数方程还可以写为      = = =    z b y a x a sin cos ( , )    v = t b = 螺旋线的重要性质： : ,   0 → 0 + : , z b 0 → b 0 + b 上升的高度与转过的角度成正比． 即 上升的高度 h = 2b 螺距 机动 目录 上页 下页 返回 结束  = 2时

例1.将下列曲线化为参数方程表示 x2+y2=1 x2+y2+z2=9 () (2) z=va2-x2-y 3) 2x+3z=6 x2+y2-ax=0 y=0 解：(1)根据第一方程引入参数，得所求为 x=coSt y=sint (0≤t≤2π) 2=3(6-2cost) 2将第二方程变形为(x-)2+y2=4, 故所求为 (x=号+号cost y=gsint (0≤t≤2π) z=a cos t

例1. 将下列曲线化为参数方程表示: 解: (1) 根据第一方程引入参数 , (2) 将第二方程变形为 故所求为 得所求为 机动 目录 上页 下页 返回 结束

*曲面的参数方程 x=0(t) 例2.求空间曲线 T:y=w(t)(a≤t≤B)绕z轴旋转 Z=0(t) 时的旋转曲面方程 解：任取点M1(p(),yw(t),0(t)∈T,点M绕z轴旋转 转过角度0后到点M(x,y,z),则 x=vo-(t)+w-(t)cose a≤t≤B y=v-(t)+w(t)sine 2 0≤0≤2π z=0(t) 这就是旋转曲面满足的参数方程 下页返回结束

例2. 求空间曲线 : 绕 z 轴旋转 时的旋转曲面方程 . 解: 点 M1绕 z 轴旋转, 转过角度 后到点 则 机动 目录 上页 下页 返回 结束 这就是旋转曲面满足的参数方程 . *曲面的参数方程

例如，直线 y=t绕z轴旋转所得旋转曲面方程为 z=2t x=1+t2 cos 0 -00<t<+0 y=v1+t2 sin O 0≤0≤2π z=2t 消去t和0，得旋转曲面方程为 4(x2 结球

例如, 直线 绕 z 轴旋转所得旋转曲面方程为 消去 t 和  , 得旋转曲面方程为 机动 目录 上页 下页 返回 结束

x =asin o 又如，xoz面上的半圆周{y=0 (0≤p≤π) z=acoso 绕z轴旋转所得旋转曲面（即球面）方程为 x =asin o cos 0≤p≤π y=asm o sin 0≤0≤2π z=acoso 说明：一般曲面的参数方程含两个参数，形如 x=x(s,t) y=y(s,t) Z=Z(s,t) 8 下页返回结束

绕 z 轴旋转所得旋转曲面 ( 即球面 ) 方程为 又如, xoz 面上的半圆周 说明: 一般曲面的参数方程含两个参数 , 形如 机动 目录 上页 下页 返回 结束