《高等数学》课程教学资源（PPT课件）Ⅱ_第八章第四节 空间直线及其方程

第四节 第七章 空间直线及其方程 空间直线方程 二、 线面间的位置关系 下页返回结束

第四节 一、空间直线方程 二、线面间的位置关系 机动 目录 上页 下页 返回 结束 空间直线及其方程 第七章

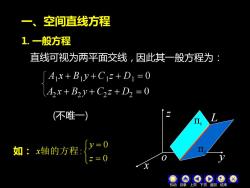
空间直线方程 1.一般方程 直线可视为两平面交线，因此其一般方程为： A1x+B1y+C12+D1=0 A2x+B2y+C22+D2=0 不唯一〉 如：x轴的方程 y=0 z=0

一、空间直线方程 x y z o 0 A1x + B1 y + C1z + D1 = 1 2 L 因此其一般方程为： 1. 一般方程 直线可视为两平面交线， (不唯一) 机动 目录 上页 下页 返回 结束    = = 0 0 : z y 如： x轴的方程

2.对称式方程 已知直线上一点Mo(x0,0,0)和它的一个方向向量 s=(m,n,p),设直线上的动点为M(x,y,z) 则 MoM∥s M(x,y,2) 故有 x-0=y-0=2-0 m n M(x0,y0,20) 此式称为直线的对称式方程（也称为点向式方程 说明：某些分母为零时，其分子也理解为零 例如，当m=n=0,p≠0时，直线方程为 x=X0 (y=yo 08 下页返回结束

( , , ) 0 0 0 0 M x y z 2. 对称式方程 故有 说明: 某些分母为零时, 其分子也理解为零. m x x − 0    = = 0 0 y y x x 设直线上的动点为 则 M (x, y,z) n y y − 0 = p z z − 0 = 此式称为直线的对称式方程(也称为点向式方程) 直线方程为 s 已知直线上一点 ( , , ) 0 0 0 0 M x y z M (x, y,z) 例如, 当 m = n = 0, p  0 时, 和它的一个方向向量 机动 目录 上页 下页 返回 结束

3.参数式方程 设 x-x0=y-0=-0 m n 得参数式方程 x=xo+mt y=y0+nt 、2=20+p1 两点式过两点P(1,1,1),P(x2,J2,2)的直线方程为： x-七1=y-1=名-1 X2-1y2-y12-Z1

3. 参数式方程 设 得参数式方程 : t p z z n y y m x x = − = − = − 0 0 0 x = x + mt 0 y = y + nt 0 z = z + p t 0 机动 目录 上页 下页 返回 结束 两点式： 过两点 ( , , ), ( , , ) 1 1 1 1 2 2 2 2 P x y z P x y z 的直线方程为： 2 1 1 2 1 1 2 1 1 z z z z y y y y x x x x − − = − − = − −

例1.用对称式及参数式表示直线 了x+y+z+1=0 2x-y+3z+4=0 解先在直线上找一点. 令x=1,解方程组 6得y=0,=2 故(1,0，-2)是直线上一点 再求直线的方向向量s 已知直线的两平面的法向量为 万=，1,1)，2=(2，-1,3) 寸1乃，s1元2=%xm 机动 上页下页返回结束

例1.用对称式及参数式表示直线 解:先在直线上找一点. 3 6 2 − = + = − y z y z 再求直线的方向向量 令 x = 1, 解方程组 ,得 y = 0, z = −2 已知直线的两平面的法向量为 是直线上一点 . s. 1 2  s ⊥ n ,s ⊥ n 1 2  s = n  n 机动 目录 上页 下页 返回 结束

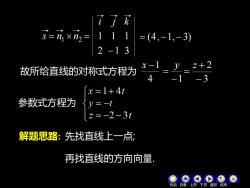
方 s=nxn= 111 =(4,-1,-3) 2-13 故所给直线的对称式方程为 2+2 x=1+4i 参数式方程为{y=-t z=-2-3t 解题思路：先找直线上一点； 再找直线的方向向量

故所给直线的对称式方程为 参数式方程为 4 x −1 −1 = y 解题思路: 先找直线上一点; 再找直线的方向向量. = (4,−1,− 3) 1 2 s = n  n 2 1 3 1 1 1 − = i j k 机动 目录 上页 下页 返回 结束

例2将直线的标准方程：x-1_y+2=乙-2 0 23 化成一般式方程。 解： x-1=0 y+23-2 02 3 x-1=0 解得 3y-2z+10=0

例 2 将直线的标准方程： 3 2 2 2 0 1 − = + = x − y z 化成一般式方程。 解：     − = + − = 3 2 2 2 1 0 y z x 解得    − + = − = 3 2 10 0 1 0 y z x 机动 目录 上页 下页 返回 结束

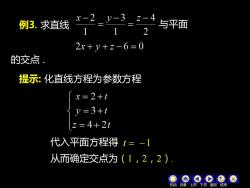
例3.求直线 x-2_y-3_2-4 与平面 1 2 2x+y+z-6=0 的交点. 提示：化直线方程为参数方程 x=2+t y=3+t z=4+2t 代入平面方程得t=-1 从而确定交点为（1,2,2) 机动 汉▣ 结

例3. 求直线 与平面 的交点 . 提示: 化直线方程为参数方程 代入平面方程得 t = −1 从而确定交点为（1，2，2）. 机动 目录 上页 下页 返回 结束

例4一直线过点A(2,-3,4),且和y轴垂直相交 求其方程. 解 因为直线和y轴垂直相交， 设交点为BO,b,0),则ABLj 故B(0,-3,0), 取5=BA={2,0,4}, 所求直线方程 x-2y+3 上页下页返回结辣

例 4 一直线过点A(2,−3,4)，且和 y轴垂直相交， 求其方程. 解 因为直线和 y轴垂直相交, (0, 3, 0) , 0 ,0) , − ⊥ B B b AB j 故 设交点为 （ ， 则   取 s = BA  = {2, 0, 4}, 所求直线方程 . 4 4 0 3 2 2 − = + = x − y z 机动 目录 上页 下页 返回 结束

二、线面间的位置关系 1.两直线的夹角 两直线的夹角指其方向向量间的夹角（通常取锐角） 设直线L1,L,的方向向量分别为 Si=(m1,h1,p1),s2=(m2,2,p2） 则两直线夹角φ满足 s2 C0S0= mim2+nn2 pip2 ym1"+n"+Pm2"+n2"p2 返回

L2 L1  二、线面间的位置关系 1. 两直线的夹角 则两直线夹角  满足 1 2 设直线 L , L = 两直线的夹角指其方向向量间的夹角(通常取锐角) 的方向向量分别为 1 2 1 2 1 2 m m + n n + p p 2 1 2 1 2 1 m + n + p 2 2 2 2 2 2 m + n + p 1 2 1 2 cos s s s  s  = 1s 2s 机动 目录 上页 下页 返回 结束