《高等数学》课程教学资源（课件讲稿）第九章_D9_2偏导数

第九章 第二节 偏导数 一、 偏导数概念及其计算 二、高阶偏导数 HIGH EDUCATION PRESS 机动 目录 返回 结

第二节 机动 目录 上页 下页 返回 结束 一、 偏导数概念及其计算 二 、高阶偏导数 偏 导 数 第九章

偏导数定义及其计算法 定义1.设函数z口f(x,y)在点(xo,yo)的某邻域内 极限 lim f(o☐☐x,yo)口f(x0,yo) 0x00 ■X 存在，则称此极限为函数z口f(x,y)在点(xo,yo)对x 的偏导数，记为 ☐x x0,yo) x(00)2x0o) f(xo.Yo);f(o-yo). 注意：f(xo,yo)日1im f(x☐☐x,yo)口f(x0,o) x口0 Ox HIGH EDUCATION PRESS 返回 结束

定义1. 在点 存在, 的偏导数，记为 的某邻域内 则称此极限为函数 极限 设函数 机动 目录 上页 下页 返回 结束 注意: 一、 偏导数定义及其计算法

同样可定义对y的偏导数 f(xo,yo)☐lim f(xo,y0☐☐y)口f(xo,yo) ▣y▣0 若函数z=f(x,y)在域D内每一点(x,y)处对x 或y偏导数存在，则该偏导数称为偏导函数，也简称为 偏导数，记为 巴.y,c)fy x’ ,2,(x,),fx,y) y HIGH EDUCATION PRESS 回

同样可定义对 y 的偏导数 若函数 z = f ( x , y ) 在域 D 内每一点 ( x , y ) 处对 x 则该偏导数称为偏导函数, 也简称为 偏导数 , 记为 机动 目录 上页 下页 返回 结束 或 y 偏导数存在

偏导数的概念可以推广到二元以上的函数 例如，三元函数u=f(x,y,)在点(x,y,2)处对x的 偏导数定义为 f(x,y,z) 口1m/xOx,ya)yx,y,z Ox▣0 O f(x,y,z)☐？ (请自己写出 f2(x,y,z)□？ HIGH EDUCATION PRESS 目录

例如, 三元函数 u = f (x , y , z) 在点 (x , y , z) 处对 x 的 偏导数的概念可以推广到二元以上的函数 . 机动 目录 上页 下页 返回 结束 偏导数定义为 (请自己写出)

二元函数偏导数的几何意义： y yo 是曲线 ?口f(x,y在点M,处的切线 y□yo 0 M,T对x轴的斜率 yy。 ）y 是曲线 口f(x,)在点M处的切线MoI,对y轴的 xxo 斜率 HIGH EDUCATION PRESS

二元函数偏导数的几何意义: 是曲线 在点 M0 处的切线 对 x 轴的斜率. 在点M0 处的切线 斜率. 是曲线 机动 目录 上页 下页 返回 结束 对 y 轴的

注意：函数在某点各偏导数都存在， 但在该点不一定连续 例，：fx,)2,20 日0，x2y2☐0 星然a0r/x0E00 ,0.o0y00 在上节已证f(x,y)在点(0,0)并不连续！ HIGH EDUCATION PRESS 上节例目录 返回结束

函数在某点各偏导数都存在, 显然 例如, 注意： 但在该点不一定连续. 上节例 目录 上页 下页 返回 结束 在上节已证 f (x , y) 在点(0 , 0)并不连续!

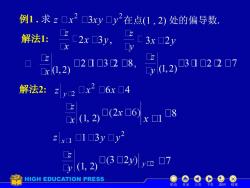
例1.求z口x2☐3xy口y在点(1,2)处的偏导数. 解法1： 号3x2y x0,2) 021口3208， a2)03102207 解法2 22口x2☐6x☐4 a,2)(2x6x18 zx1☐13y0y2 a.236u2n7 HIGH EDUCATION PRESS 返回 结

例1 . 求 解法1: 解法2: 在点(1 , 2) 处的偏导数. 机动 目录 上页 下页 返回 结束

例2.设z□xy(x□0，且x口)，求证 1 02z lnx☐y 证：口 Bz CxInx Cx Cy x■Z 1 ☐x'口x☐2z lnx☐y 例3.求r口x2☐y2口z2 的偏导数 2x 解： 2x20y20z2 HIGH EDUCATION PRESS 目录

例2. 设 证: 例3. 求 的偏导数 . 解: 求证 机动 目录 上页 下页 返回 结束

例4.已知理想气体的状态方程pP口RT(R为常数)， 求证 □1 RT 证： p RT 说明：此例表明， RT 偏导数记号是一个 整体记号，不能看作 分子与分母的商！ T R □p R RT HIGH EDUCATION PRESS 返回 结

偏导数记号是一个 例4. 已知理想气体的状态方程 求证: 证: 说明: (R 为常数) , 不能看作 分子与分母的商 ! 此例表明, 机动 目录 上页 下页 返回 结束 整体记号

二、高阶偏导数 设z=f(x,y)在域D内存在连续的偏导数 f,(x) □y 若这两个偏导数仍存在偏导数，则称它们是：=f(x,y〉 的二阶偏导数.按求导顺序不同，有下列四个二阶偏导 数 口fxx,y方 f(.y) 回f(x,y HIGH EDUCATION PRESS 回 结

二、高阶偏导数 设 z = f (x , y)在域 D 内存在连续的偏导数 若这两个偏导数仍存在偏导数，则称它们是z = f ( x , y ) 的二阶偏导数 . 按求导顺序不同, 有下列四个二阶偏导 机动 目录 上页 下页 返回 结束 数: