《高等数学》课程教学资源（PPT课件）第十二章_D12_2数项级数及审敛法.ppt

第二节 第十二章 常款项级赵的审敘法 正项级数及其审敛法 二、交错级数及其审敛法 三、绝对收敛与条件收敛 HIGH EDUCATION PRESS 机动目录上页下页返回结束

二、交错级数及其审敛法 三、绝对收敛与条件收敛 第二节 一、正项级数及其审敛法 常数项级数的审敛法 机动 目录 上页 下页 返回 结束 第十二章

正项级数及其审敛法 00 若4，≥0，则称∑4n为正项级数 n= 定理1.正项级数》4n收敛二 部分和序列Sm n=. (n=1,2,.)有界 证：“一”若∑n收敛，则{Sn}收敛，故有界 n=1 :4n≥0，∴.部分和数列{n}单调递增 又已知{Sn}有界故{Sn}收敛，从而∑4n也收敛 n=l HIGH EDUCATION PRESS 机动目录上页下页返回结束

一、正项级数及其审敛法 若  0, n u   n=1 un 定理 1. 正项级数 收敛 部分和序列 有界 . 若 收敛 , ∴部分和数列 又已知 有界, 故 从而 故有界. 则称 为正项级数 . 单调递增, 收敛 , 也收敛. 证: “ ” “ ” 机动 目录 上页 下页 返回 结束

00 定理2比较审敛法) 设∑4n,∑'n是两个正项级数 n=1n=1 且存在NeZ+,对一切n>N,有un≤kyn(常数k>0) 则有 (①)若强级数∑yn收敛，则弱级数∑”n也收敛： n=1 n=l 00 (2)若弱级数 ∑n发散，则强级数∑Vn也发散 n=1 n=1 证：因在级数前加、减有限项不改变其敛散性，故不妨 设对一切neZ+,都有un≤kvn, 令S,和on分别表示弱级数和强级数的部分和，则有 HIGH EDUCATION PRESS Oe0C08 机动目录上页下页返回结束

都有 定理2 (比较审敛法) 设 且存在 对一切 有 (1) 若强级数 则弱级数 (2) 若弱级数 则强级数 证: 设对一切 则有 收敛 , 也收敛 ; 发散 , 也发散 . 分别表示弱级数和强级数的部分和, 则有 是两个正项级数, (常数 k > 0 ), 因在级数前加、减有限项不改变其敛散性, 故不妨 机动 目录 上页 下页 返回 结束

Sn≤kon 00 (1)若强级数∑yn收敛，则有o=1imon n-→o0 n=1 因此对一切neZ,有Sn≤ko 由定理1可知，弱级数∑4n也收敛 n=1 (2)若弱级数∑4n发散，则有1imSn=∞， n=] n→0 因此1imon=o,这说明强级数∑'n也发散 n→0 n=1 HIGH EDUCATION PRESS 机动目录上 下页返回结

(1) 若强级数 则有 因此对一切 有 由定理 1 可知, (2) 若弱级数 则有 因此 这说明强级数 也发散 . 也收敛 . 发散, 收敛, 弱级数 机动 目录 上页 下页 返回 结束

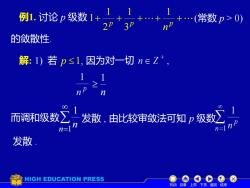
例1.讨论p级数1+ 2P 的敛散性 解：1)若p≤1，因为对一切n∈Z, 而调和级数∑发散，由比较审敛法可知p级数∑ n=] n= 发散 HIGH EDUCATION PRESS 机动目录上页下页返回结束

例1. 讨论 p 级数 + p + p ++ p + n 1 3 1 2 1 1 (常数 p > 0) 的敛散性. 解: 1) 若 p 1, 因为对一切 而调和级数   =1 1 n n 由比较审敛法可知 p 级数 n 1  发散 . 发散 , 机动 目录 上页 下页 返回 结束

2)若p>1,因为当n-1≤x≤n时 xb, 故 so] a{a n→o0 故强级数收敛，由比较审敛法知p级数收敛 HIGH EDUCATION PRESS 机动目录上页下页返回结束

p 1, 因为当 , 1 1 p p n x  故  − = n p n p x n n 1 d 1 1  −  n n p x x 1 d 1   − −   − = −1 −1 1 ( 1) 1 1 1 p p p n n 考虑强级数   − −   − −  =  1 1 2 1 ( 1) 1 p p n n n 的部分和  n   + −   = − − =  1 1 1 ( 1) 1 1 p p n k k k n →  故强级数收敛 , 由比较审敛法知 p 级数收敛 . 时, 1 ( 1) 1 1 − + = − p n       + + + −       + −       − −1 −1 −1 −1 −1 ( 1) 1 1 3 1 2 1 2 1 1 p p p p p n n  1 2) 若 机动 目录 上页 下页 返回 结束

调和级数与p级数是两个常用的比较级数 若存在NeZ,对-切n≥N, (n≥。，则∑n发散： 00 n=1 ②)：≤>则，收敛 n=1 HIGH EDUCATION PRESS DeOC①8 机动目录上页下页返回结束

调和级数与 p 级数是两个常用的比较级数. 若存在 , + N  Z 对一切 n  N , 机动 目录 上页 下页 返回 结束

例2.证明级数 n+D 发散 证：因为 n+1 (n=1,2,.〉 而级数 发散 根据比较审敛法可知，所给级数发散 HIGH EDUCATION PRESS 十 机动目录上页下页返回结束

证明级数 发散 . 证: 因为 2 ( 1) 1 ( 1) 1 +  n n + n 而级数   = = 2 1 k k 发散 根据比较审敛法可知, 所给级数发散 . 例2. 机动 目录 上页 下页 返回 结束

定理3.（比较审敛法的极限形式） 设两正项级数 00 00 ∑4n,∑m满足lm4n=乙，则有 n=1 n=1 n->oo Vn (1)当0≤10,存在N∈Z+,当n>N时， -小水(1 HIGH EDUCATION PRESS 机动目录上页下页返回结束

定理3. (比较审敛法的极限形式) lim l, v u n n n = → 则有 两个级数同时收敛或发散 ; (2) 当 l = 0 (3) 当 l =∞ 证: 据极限定义, 设两正项级数 满足 (1) 当 0 < l <∞ 时, 机动 目录 上页 下页 返回 结束

(l-E)vn≤4n≤(l+e)vn (n>N) 00 (1)当0N),由定理2知 若∑ym收敛，则∑un也收敛： n=l n=1 (3)当1=时，存在NeZ*,当n>N时，”n>1,即 un >Vn oO 由定理2可知，若∑Vm发散，则∑un也发散 n=] n=] HIGH EDUCATION PRESS 机动目 下页返回结束

n n n (l − )v  u  (l +  ) v 由定理 2 可知   n=1 n v 同时收敛或同时发散 ; (n  N ) (3) 当l = ∞时, 即 n n u v 由定理2可知, 若   n=1 n v 发散 , (1) 当0 < l <∞时, (2) 当l = 0时, 由定理2 知   n=1 n 若 v 收敛 , 机动 目录 上页 下页 返回 结束