《高等数学》课程教学资源（PPT课件）Ⅱ_D10_2二重积分的计算

第九章第二节二重积分的计算法利用直角坐标计算二重积分利用极坐标计算二重积分二重积分的换元法一AD-

*三、二重积分的换元法 第二节 一、利用直角坐标计算二重积分 二、利用极坐标计算二重积分 机动 目录 上页 下页 返回 结束 二重积分的计算法 第九章

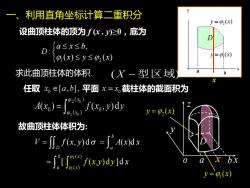
y利用直角坐标计算二重积分y=p2(x)设曲顶柱体的顶为f(x，J)>0，底为Ia<x<b,D=pi(x)(0(x)≤y≤p2(x)xa求此曲顶柱体的体积b(X-型区域?任取xE[a,b]，平面x=x.截柱体的截面积为192（0）A(x0)= [0() (xo, y)dyy=(2(x)Oxo故曲顶柱体体积为：V= JJ,f(x,y)do =[' A(x)d xP21xbxXa02d f(x,y)dy jd xy=(p(x)

[ ]d x b a = x  求此曲顶柱体的体积. 设曲顶柱体的顶为 f (x , y)≥0，底为 1 2 , : ( ) ( ) a x b D   x y x        任取 平面 故曲顶柱体体积为: ( , ) d D V f x y =   2 1 ( ) ( ) ( , ) d x x f x y y   ( )d b a = A x x  截柱体的截面积为 2 y x =  ( ) 1 y x =  ( ) z x y o a b D 一、利用直角坐标计算二重积分 2 y x =  ( ) a b D 1 y x =  ( ) x (X −型区域)

[c≤y<d,同样，若曲顶柱体的底为(y(y)≤x≤y2(y)y则其体积可按如下两次积分计算dV= J, f(x, y)dox±y2(y)J'1 [wa) f(x, y)dx Jdy福Exy2f(x,y)dxdyJyi(y)(Y一型区域)

y d c o x 2 x y = ( ) 1 x y = ( ) y [ ] d d c = y  1 2 , : ( ) ( ) c y d D   y x y        同样, 若曲顶柱体的底为 则其体积可按如下两次积分计算 ( , ) d D V f x y =   2 1 ( ) ( ) ( , ) d y y f x y x   (Y −型区域)  = d c d y

由曲顶柱体体积的计算可知,当被积函数f(x,J)≥0若D为 X-型区域且在D上连续时，=P2(x)-Pi(x)≤y≤P2(x)Da≤x≤bday=pi(x)b xR.br2(x)则 ,f(x,y)dxdydxlf(x, y)dyJaJpi(x)yx =2(y)yi(y)≤x≤y2(y)d若D为Y-型区域Dyc≤≤dx=VlC2)则(, f(x,y)dxdy =dy(x, y)dxoxJ目录结束动质返回

且在D上连续时, 当被积函数 f (x, y)  0        a x b x y x D ( ) ( ) : 1  2 D f (x, y)dx dy f x y y x x ( , )d ( ) ( ) 2 1     = b a d x 由曲顶柱体体积的计算可知, 若D为 X – 型区域 则 ( ) 1 y =  x ( ) 2 y =  x o b x y D a x 若D为Y –型区域        c y d y x y D ( ) ( ) : 1  2 y ( ) 1 x = y ( ) 2 x = y x d o c y f x y x y y ( , )d ( ) ( ) 2 1     d c 则 d y 机动 目录 上页 下页 返回 结束

说明：（1)若积分区域既是X-型区域又是Y-型区域则有(, f(x, y)dxdyy=2(x)r2(x)2(y)X=V(y)x =f(x,y)dydxDJ@i(x)1Pi(x)Y=y 2(y)Cf (x, y)dxtbxQJyi(y)为计算方便，可选择积分次序，必要时还可以交换积分次序2(2）若积分域较复杂,可将它分成若于DDX-型域或Y-型域，则DJ。 = J, + , +J,AUX-

o x y 说明: (1) 若积分区域既是X–型区域又是Y –型区域 , D f (x, y)dx dy 为计算方便,可选择积分次序, 必要时还可以交换积分次序. ( ) 2 y =  x o x y D a b ( ) 1 x = y ( ) 2 x = y d c 则有 x ( ) 1 y =  x y f x y y x x ( , )d ( ) ( ) 2 1     = b a d x f x y x y y ( , )d ( ) ( ) 2 1     = d c d y (2) 若积分域较复杂,可将它分成若干 D1 D2 D3 X-型域或Y-型域 ,     = + + D D1 D2 D3 则 机动 目录 上页 下页 返回 结束

例1.计算I=(Cxyd,其中D是直线y=1,x=2,及=x 所围的闭区域1≤y≤x解法1.将D看作X-型区域，则D1≤x≤2I =? d x[ xyd y= ["[Ixy? ]dsx IdxC(y≤x≤2解法2.将D看作Y-型区域，则D：1≤y≤2=(Tix?y]'dy=0xVd x =小结束XL

x y 2 1 1 y = x o 2  = 2 1 dy 例1. 计算 d ,  = D I xy  其中D 是直线 y＝1, x＝2, 及 y＝x 所围的闭区域. x 解法1. 将D看作X–型区域, 则    D : I =  2 1 d x xyd y  = 2 1 d x    = − 2 1 2 3 1 2 1 x x dx 8 9 =   1 2 2 1 x xy 解法2. 将D看作Y–型区域, 则    D : I =  xyd x  2 1 d y   y x y 2 2 2 1    = − 2 1 3 2 1 2y y dy 8 9 = y 1 x y 2 1  y  x 1  x  2 y  x  2 1  y  2 机动 目录 上页 下页 返回 结束

例2. 计算I =[,y1+x?-ydo，其中D是直线y=x，y=xx=-1及V=1所围的闭区域解法1.如图，将D看作X-型区域，则Ldx/V+x?-y?dyV=y=x解法2.如图，将D看作Y-型区域，则-I =[ dy, yi+x? -y dx（较繁琐

2 2 1 d , D I y x y = + −  例  2. 计算 其中D 是直线 y＝x , x＝-1 及 y＝1 所围的闭区域 . y x = x y o 1 1 y=1 -1 x=-1 解法1. 如图， 1 1 2 2 1 1 x I dx y x y dy − = + −   将D看作X–型区域 , 则 解法2.如图， 1 2 2 1 1 1 y I dy y x y dx − − = + −   将D看作Y–型区域 , 则 -1 y x = x y o 1 1 y=1 -1 x=-1 （较繁琐） 2 1 =

l，xydo，其中D是抛物线=x及直线例3.计算1V= x-2 所围成的闭区域解：为计算简便，先对x后对积分[?≤x≤+2则福4 x-1≤≤2y=x-2V+2xydo = [' dyf2 xydxx?/+dy=-yidyV+吉束

例3. 计算 d , D xy  其中D 是抛物线 所围成的闭区域. 解: 为计算简便, 先对 x 后对 y 积分,    D :  xy d x  D xyd − = 2 1 dy   − + = 2 1 2 2 2 1 x y 2 dy y y − = + − 2 1 2 5 [ ( 2) ] d 2 1 y y y y D y = x 2 y = x − 2 2 −1 4 o y x y 2 2 y  x  y + −1  y  2 2 y y + 2 及直线 则 机动 目录 上页 下页 返回 结束

sin x例4.计算dxdy,其中D是直线y=x,y=D子x=元所围成的闭区域解：由被积函数可知，先对x积分不行X=元因此取D为X-型域元OX[0≤y≤x10≤≤元sin x元sinxdxdyady10Cxsin x dx = [- cos x ]A-E

例4. 计算 d d , sin D x y x x 其中D 是直线 所围成的闭区域. o x y D  x =  y = x 解: 由被积函数可知, 因此取D 为X – 型域 :        x  y x D 0 0 :  D x y x x d d sin  x y 0 d  =  0 sin x dx = 2  =  0 d sin x x x 先对 x 积分不行, 机动 目录 上页 下页 返回 结束

1练习.1.计算e' dxdy,y2=x直线其中D是抛物线JJD(答案:二)x=0,J=1所围成的闭区域?[-1<x<12.计算y-xdxdy,其中 D:0≤y≤1(答案：y≤x≤y3.计算其中 Dex dxdy,0≤y≤l(答案：说明：有些二次积分为了积分方便，还需交换积分次序AA目录机动上页下页返回结束

练习.1. 计算 d d , D y x e x y 其中D 是抛物线 所围成的闭区域. 2. 计算      −   0 1 1 1 : y x 其中 D 说明: 有些二次积分为了积分方便, 还需交换积分次序. 机动 目录 上页 下页 返回 结束 直线 d d , 2  − D y x x y 3. 计算 d d , D x y e x y 其中        0 1 : y y x y D