《高等数学》课程教学资源（PPT课件）Ⅱ_D11_4对面积的曲面积分

第十章第四节对面积的曲面积分对面积的曲面积分的概念与性质对面积的曲面积分的计算法-下页返回洁乐

第四节 一、对面积的曲面积分的概念与性质 二、对面积的曲面积分的计算法 机动 目录 上页 下页 返回 结束 对面积的曲面积分 第十章

对面积的曲面积分的概念与性质一、引例：设曲面形构件具有连续面密度p（x,y,z),求质量M类似求平面薄板质量的思想，采用(Ek,Nk,Sk)分割，近似，求和，取极限的方法，可得ZnM =limZp(5k,nk,Sk)ASkO2→0 k=1yX其中，入表示n小块曲面的直径的最大值（曲面的直径为其上任意两点间距离的最大者）O00机动目录上页下页返回结束

o x y z 一、对面积的曲面积分的概念与性质 引例: 设曲面形构件具有连续面密度 类似求平面薄板质量的思想, 采用 可得  = n k 1 M = ( , , )  k k  k 求质 分割，近似，求和，取极限 的方法 ,  量 M. 其中,  表示 n 小块曲面的直径的 最大值 (曲面的直径为其上任意两点间距离的最大者). 机动 目录 上页 下页 返回 结束

定义：设Z为光滑曲面，f(xyz)是定义在上的个有界函数，若对乙做任意分割和局部区域任意取点乘积和式极限2记作 (I f(x,y,z)dSlimZ(5k, nk,5k)AS,记20k=1>都存在,则称此极限为函数f(x,y,z)在曲面Z上对面积的曲面积分或第一类曲面积分.其中f(x,J,z)叫做被积函数，乙叫做积分曲面曲面形构件的质量为 M =(p(x,,z)dS据此定义，Eds曲面面积为 S=l_000-洁乐

M (x, y,z)d S  =  定义: 设  为光滑曲面, “乘积和式极限” 都存在, 的曲面积分   f (x, y,z)d S 其中 f (x, y, z) 叫做被积 据此定义, 曲面形构件的质量为 曲面面积为 f (x, y, z) 是定义在  上的一 个有界函数, 记作 或第一类曲面积分. 若对  做任意分割和局部区域任意取点, 则称此极限为函数 f (x, y, z) 在曲面  上对面积 函数,  叫做积分曲面. 机动 目录 上页 下页 返回 结束

对面积的曲面积分与对弧长的曲线积分性质类似积分的存在性．若f(x,y,z)在光滑曲面Z上连续则对面积的曲面积分存在·对积分域的可加性．若Z是分片光滑的，例如分成两片光滑曲面Z1,2，则有[ f(x,y,z)dS =Jf f(x, y,z)dS + Jfz, f(x, y,z)ds·线性性质设kj,k2为常数,则[,[kif(x, y,z)± k2g(x, y,z)]d S= ki (/ f(x, y,z)dS± k2 (/g(x, y,z)dseODO目录返回结束机动FI质

则对面积的曲面积分存在. • 对积分域的可加性. , , 1 2 则有 =  f (x, y,z)d S 1 f (x, y,z)d S    k f (x, y,z)  k g(x, y,z) d S 1 2 • 线性性质.     = k f (x, y,z)dS  k g(x, y,z)dS 1 2 在光滑曲面  上连续, 对面积的曲面积分与对弧长的曲线积分性质类似. • 积分的存在性. 若  是分片光滑的, 例如分成两 片光滑曲面 机动 目录 上页 下页 返回 结束

二、对面积的曲面积分的计算法定理：讠设有光滑曲面Z:z =z(x,y),(x,y)e Dxyf(x,,z)在Z上连续，则曲面积分D[f(x,y,z)dS 存在,且有[[, f(x, y,z)ds(△0k)xy(Ek,nk,Sk)(/f(x, y,z(x, y) / 1+ zx (x,y)+ z,?(x, y)dxdy证明：由定义知nJ, (x,y,z)dS = limf(Ek,nkSk)ASk10k=0000-E

o x y z 定理: 设有光滑曲面 f (x, y, z) 在  上连续,  存在, 且有  f (x, y,z)dS  = Dxy f (x, y, ) 二、对面积的曲面积分的计算法 则曲面积分 证明: 由定义知  = n k 1 0 lim → Dxy ( , , )  k k  k k x y ( )  机动 目录 上页 下页 返回 结束

而 △Sk=+ zx(x, y)+z,(x, y)dxd y[1+ zx?(Ek, nk)+zy2(5k, nh)(A0k)xy f(x, y,z)dsf(Ek,nk,z(k,nk)lim0K=[1+ z2(Ek, nk)+2,2(5k, nk)(Aok)xylim(光滑)=E f(Ek,nk,z(Ek,nk))元->0A/1+ zx?(Ek, nk)+z,2(Ek, nk)(A0k)xyf(x, y, z(x, y) )/ 1+zx(x, y)+z,?(x, y)dxdyx1小1区回结束

z x y z x y x y k x y 1 x ( , ) y ( , ) d d ( ) 2 2   + +  x k k y k k k xy 1 z ( , ) z ( , )( ) 2 2 = +   +    x k k y k k k xy 1 z ( , ) z ( , )( ) 2 2 +   +    x k k y k k k xy 1 z ( , ) z ( , )( ) 2 2 +   +    f x y z x y z x y x y x y Dx y ( , , ) 1 ( , ) ( , )d d 2 2 = + +  ( , , ( , )) k k k k f   z   ( , , ( , )) k k k k f   z     f (x, y,z)dS 而 (光滑) 机动 目录 上页 下页 返回 结束

说明：1)如果曲面方程为x = x(y,2), (y,2)e Dy2或 y=(x,z2),(x,z)eD)可有类似的公式2)若曲面为参数方程，只要求出在参数意义下dS的表达式，也可将对面积的曲面积分转化为对参数的二重积分.（见本节后面的例4,例5)O00E

说明: Dyz x = x( y,z), ( y,z) Dxz 或 y = y(x,z), (x,z) 可有类似的公式. 1) 如果曲面方程为 2) 若曲面为参数方程, 只要求出在参数意义下dS 的表达式 , 也可将对面积的曲面积分转化为对参数的 二重积分. (见本节后面的例4, 例5) 机动 目录 上页 下页 返回 结束

dsJI,例1.计算曲面积分其中是球面1Z截出的顶部=α2被平面z=h(0<h<a)解: Z:z= /α2-x2 -2(x,y)eD)adxdyDL2元a二no2元 aln2动自结束

Dxy 例1. 计算曲面积分 其中是球面 被平面 截出的顶部. 解: 2 2 2 2 D : x y a h xy +  − 2 2 1 x y + z + z   z d S  =   2 0 a d 0 ln( ) 2 1 2 2 2 2 2 a h a a +    − −    =    − − = Dx y a x y a x y 2 2 2 d d  − − 2 2 0 2 2 a h d a    o x z y  h a 机动 目录 上页 下页 返回 结束

思考：若是球面=α被平行平面z=±h 截12+7出的上下两部分，则0OX(9元)练习1.P222题15 (2)A-店

思考: 若  是球面 被平行平面 z =±h 截 出的上下两部分, ( ) d =   z S ( ) d =   z S 0 h 4 ln a  a 则 h − h  o x z y  机动 目录 上页 下页 返回 结束 练习1. P222题 5 (2)

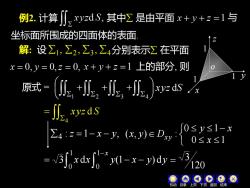
例2. 计算[_xyzdS,其中Z是由平面x+y+z=1与坐标面所围成的四面体的表面解：设Z，Z2,Z3,4分别表示Z在平面x=0,y=0,z=0,x+y+z=1 上的部分,则原式=J2, +, +2, +xyz dxyzds[0≤y≤1-xZ4 :z=1-x-y, (x,y)eDxy :0≤x≤1C1-"y(1-x-y)dy= V3/xdxI1200AOO目录返回结束-1质

例2. 计算 其中 是由平面 坐标面所围成的四面体的表面. o z y x 1 1 1 解: 设 上的部分, 则 1 2 3 4  ,  ,  ,      = 4 xyz d S : 1 , 4  z = − x − y        −  0 1 0 1 ( , ) : x y x x y Dxy  − − − x y x y y 1 0 (1 ) d 120 3 = 与  = 1 0 3 x dx         + + + 1 2 3 4  xyz dS  原式  = 分别表示 在平面 机动 目录 上页 下页 返回 结束