《高等数学》课程教学资源（PPT课件）Ⅱ_第九章 第八节 多元函数的极值及其求法

第八章第节多元函数的极值及其求法多元函数的极值最值应用问题三、条件极值AOC-下页返回结乐

第八章 第八节 一、多元函数的极值 二、最值应用问题 三、条件极值 机动 目录 上页 下页 返回 结束 多元函数的极值及其求法

最小值多元函数的极值及最大、定义：若函数 z=f(x,y)在点 P(xo,yo)的某去心邻域内有f(x,y) f(xo,yo))则称函数在该点取得极大值(极小值)极大值和极小值统称为极值使函数取得极值的点称为极值点可推广到n元函数

一、 多元函数的极值及最大、最小值 则称函数在该点取得极大值 极大值和极小值 统称为极值, 使函数取得极值的点称为极值点. 定义: 若函数 在点 P x y 0 0 0 ( , ) 的某 去心邻域内有 (极小值). 0 0 ( ) f x y f x y ( , ) ( , )  可推广到 n 元函数

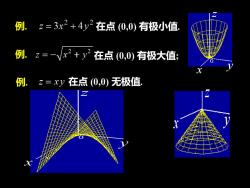
例.z=3x2+4y2在点(0,0)有极小值例z = -/x? + y2在点（0,0)有极大值；例z=xy在点(0,0)无极值

x y z 例. 在点 (0,0) 有极小值. 在点 (0,0) 有极大值; 在点 (0,0) 无极值. x y z x y z 例. 例.     

定理1(必要条件）函数z=f(x,y)在点(xo,yo)存在偏导数，且在该点取得极值，则有fi(xo, yo) = 0, f,(xo,yo)= 0证：因z=f(x,y)在点（xo,yo）取得极值，故z=f(x,yo)在 x=xo取得极值z=f(xo,)在y=yo取得极值据一元函数极值的必要条件可知定理结论成立[f’(x,J) = 0使称为驻点的点(xo,yo),)(x,J) =0 的注：驻点不一定是极值点

称为驻点 . 定理1 (必要条件) 函数 偏导数, 证: 据一元函数极值的必要条件可知定理结论成立. ( , ) 0 , ( , ) 0 f x x0 y0 = f y x0 y0 = 取得极值 , 取得极值 取得极值 且在该点取得极值 , 则有 存在 故 0 0 0 0 ( , ) ( , ) ( , )   =   =  使 x 的点 ， y f x y x y f x y 注：驻点不一定是极值点

定理2(充分条件）若函数z=f(x,J)在点（xo,Jo）的的某邻域内具有一阶和二阶连续偏导数，且fx(xo , yo)= 0 , J,(xo , yo) = 0令 A= fxx(xo,yo), B= fxy(xo,yo), C = fyy(xo,yo)A0时,具有极值A>0时取极小值2)当AC-B2<0时,没有极值3)当 AC-B2=0时,不能确定需另行讨论证明见第九节(P123)000--

时, 具有极值 定理2 (充分条件) 的某邻域内具有一阶和二阶连续偏导数, 且 令 则: 1) 当 A0 时取极小值. 2) 当 3) 当 证明见 第九节(P123) . 时, 没有极值. 时, 不能确定 , 需另行讨论. 若函数 z = f (x, y) 在点 (x0 , y0 ) 的 ( , ) 0 , ( , ) 0 f x x0 y0 = f y x0 y0 = ( , ) , ( , ) , ( , ) 0 0 0 0 0 0 A f x y B f x y C f x y = x x = x y = y y 0 2 AC − B  0 2 AC − B  0 2 AC − B = 机动 目录 上页 下页 返回 结束

例1.讨论函数z=x3+及z=(x2+)在点(0,0)是否取得极值解：显然(0,0)都是它们的驻点，并且在(0,0)都有AC-B2= 0z=x3 +y3在(0,0)点邻域内的取值正可能为负，因此 z(0,0)不是极值0当x2 +2 0时, z=(x2 +)>(0.0) =0因此 z(0,0)=(x2 +2)[(0.0)=0为极小值AH机动目录返回结束上页下页

例1.讨论函数 及 是否取得极值. 解: 显然 (0,0) 都是它们的驻点 , 在(0,0)点邻域内的取值 , 因此 z(0,0) 不是极值. 因此 0 , 当x 2 + y 2  时 2 2 2 z = (x + y ) 0  z (0,0) = 为极小值. 正 负 0 在点(0,0) x y z o 并且在 (0,0) 都有 可能为 机动 目录 上页 下页 返回 结束

例2.求函数f(x,)=x3-3+3x2+329x的极值解：第一步求驻点Jx(x,y)=3x2 +6x- 9= 0解方程组J,(x,y)= -3y2 +6y = 0得驻点：(1,0)，(1,2),(-3,0)，（-3,2)CB第二步判别．求二阶偏导数Jxx(x,y)=6x+6, fxy(x,y)= 0, fyy(x,y)= -6y+ 6在点(1,0)处A=12,B=0,C=6.AC-B2=12×6>0, A>0,:f(1,0)=-5为极小值;0000-E

例2. 求函数 解: 第一步 求驻点. 得驻点: (1, 0) , (1, 2) , (–3, 0) , (–3, 2) . 第二步 判别. 在点(1,0) 处 为极小值; 解方程组 A B C 的极值. 求二阶偏导数 f (x, y) = 6x + 6, xx f (x, y) = 0, x y f (x, y) = −6 y + 6 y y 12 6 0, 2 AC − B =   A  0, 机动 目录 上页 下页 返回 结束

在点(1,2)处 A=12,B=0,C=-6AC-B2 =12×(-6)0, A<0,:.f(-3,2)=31为极大值fxx(x,y)=6x+6, fx,(x,y)=0, fyy(x,y)= -6y+6BAC大公区回结束

在点(−3,0) 处 不是极值; 在点(−3,2) 处 为极大值. f (x, y) = 6x + 6, xx f (x, y) = 0, x y f (x, y) = −6 y + 6 y y 12 6 0, 2 AC − B = −   12 ( 6) 0, 2 AC − B = −  −  A  0, 在点(1,2) 处 12 ( 6) 0, 不是极值; 2 AC − B =  −  A B C 机动 目录 上页 下页 返回 结束

最值问题二、依据函数f在闭域上连续函数f在闭域上可达到最值驻点最值可疑点边界上的最值点特别，当区域内部最值存在，且只有一个极值点P时f(P)为极小(大) 值> f(P)为最小(大)值AOU

二、最值问题 函数 f 在闭域上连续 函数 f 在闭域上可达到最值 最值可疑点    驻点 边界上的最值点 特别, 当区域内部最值存在, 且只有一个极值点P 时, f (P) 为极小(大) 值 f (P) 为最小(大) 值 依据 机动 目录 上页 下页 返回 结束

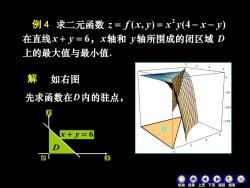
例 4 求二元函数 = f(x,)=x2y(4--)在直线x＋y=6，x轴和 y轴所围成的闭区域 D上的最大值与最小值解如右图先求函数在D内的驻点，100x+y=6DOX0000x机动目录上页下页返回结束

例 4 求二元函数 ( , ) (4 ) 2 z = f x y = x y − x − y 在直线x + y = 6，x轴和 y轴所围成的闭区域 D 上的最大值与最小值. 解 先求函数在D内的驻点， x y o x + y = 6 D D 如右图 机动 目录 上页 下页 返回 结束