《高等数学》课程教学资源（PPT课件）Ⅱ_第九章 第五节 隐函数的求导公式

第五节 第八章 隐画数的求导方法 一个方程所确定的隐函数 及其导数 方程组所确定的隐函数组 及其导数 -m 下页返回结束

第五节 第八章 机动 目录 上页 下页 返回 结束 一、一个方程所确定的隐函数 及其导数 二、方程组所确定的隐函数组 及其导数 隐函数的求导方法

本节讨论： 1)方程在什么条件下才能确定隐函数 例如，方程x2+√少+C=0 当C0时，不能确定隐函数 2)在方程能确定隐函数时，研究其连续性、可微性 及求导方法问题

本节讨论 : 1) 方程在什么条件下才能确定隐函数 . 例如, 方程 当 C 0 时, 不能确定隐函数; 2) 在方程能确定隐函数时, 研究其连续性、可微性 及求导方法问题 . 机动 目录 上页 下页 返回 结束

一、一个方程所确定的隐函数及其导数 定理1.设函数F(x,y在点P(xo,yo的某一邻域内满足 ①具有连续的偏导数： ②F(x0,0)=0: ③F,(x0,0)≠0 则方程F(x,y)=0在点x的某邻域内可唯一确定一个 单值连续函数y=f(x,),满足条件yo=f(x0),并有连续 导数 (隐函数求导公式) dx F 定理证明从略，仅就求导公式推导如下： 上页下页返回结球

一、一个方程所确定的隐函数及其导数 定理1. 设函数 ( , ) 0; F x0 y0 = 则方程 单值连续函数 y = f (x) , 并有连续 y x F F x y = − d d (隐函数求导公式) 定理证明从略，仅就求导公式推导如下： ① 具有连续的偏导数; 的某邻域内可唯一确定一个 在点 的某一邻域内满足 ( , ) 0 Fy x0 y0  ② ③ 满足条件 机动 目录 上页 下页 返回 结束 导数

设y=f(x)为方程F(x,y)=0所确定的隐函数，则 F(x,f(x)≡0 两边对x求导 oF oF dy 三0 Ox Oy dx 在(x,yo)的某邻域内F,≠0

两边对 x 求导 y x F F x y = − d d  0 在 的某邻域内 Fy 则 机动 目录 上页 下页 返回 结束

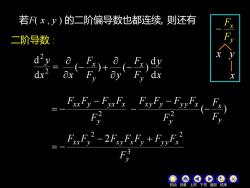
若F(x,y)的二阶偏导数也都连续，则还有 二阶导数： sy- FxFy2-2FxyExEy+FyyFx2 下页返回结束

若F( x , y ) 的二阶偏导数也都连续, = 2 2 d d x y 2 y xx y yx x F F F − F F = − 3 2 2 2 y xx y x y x y y y x F F F − F F F + F F = − y x F F − ( ) y x F F y −   + ( ) 2 y x y xy y y y x F F F F F F F − − − 二阶导数 : ( ) y x F F x −   x y x x y d d 则还有 机动 目录 上页 下页 返回 结束

例1.验证方程siny+ex-xy-1=0在点0,0)某邻域 可确定一个单值可导隐函数y=f(x),并求 d-y dxx=0’dx2x=0 解：令F(x,y)=siny+e-xy-1,则 ①F=e-y,F,=cosy-x连续 ②F0,0)=0, ③F,(0,0)=1≠0 由定理1可知，在x=0的某邻域内方程存在单值可 导的隐函数y=f(x),且

例1. 验证方程 在点(0,0)某邻域 可确定一个单值可导隐函数 d 0 d , d 0 d 2 2 = x x = y x x y 解: 令 F(x, y) = sin y + e − xy −1, x F(0,0) = 0, F e y, x x = − 连续 , 由 定理1 可知, (0,0) =1 Fy  0 ① 导的隐函数 则 F y x y = cos − ② ③ 在 x = 0 的某邻域内方程存在单值可 且 机动 目录 上页 下页 返回 结束 并求

dy F ex-y 0,x=0- =-1 dx x=0 cosyxx=0,y=0 d2y dx 2 x=0 d(e=y) dx cosy-xx=0,y=0,y'=-1 (ex-y)(cosy-x)-(e*-y)(-siny.y'-1) x=0 (cosy-x) y=0 y C8 机动 上页下页返回结束

d 0 d x x = y = 0 = − F x F y x = − cos y − x e y x − x = 0, y = 0 机动 目录 上页 下页 返回 结束 d 0 d 2 2 x x = y ) cos ( d d y x e y x x − − = − 2 ( cos ) y − x = − = −3 1 0 0  = − = = y y x ( e y ) x −  (cos y − x) (e y) x − − (−sin y  y  −1)

导数的另一求法一利用隐函数求导 siny+e*-xy-1=0,y=y(x) 两边对x求导 x=0 cosy.y'+e*-y-xy'=0 e"-y cosy-x(0,0) 两边再对x求导 =-1 -siny.(y)2+cosy.y"+e*-y'-y'-xy"=0 令x=0,注意此时y=0,y'=-1 d-v dx2x=0-3 返回

= 0  x y 3 d 0 d 2 2 = − x x = y sin y e xy 1 0, y y(x) x + − − = = 两边对 x 求导 两边再对 x 求导 − sin y ( y ) + cos y  y  2 令 x = 0 , 注意此时 y = 0 , y  = −1 cos y x (0,0) e y x − − = − 导数的另一求法 — 利用隐函数求导 机动 目录 上页 下页 返回 结束

定理2.若函数F(x,y,z)满足 ①在点P(x,y0,z0)的某邻域内具有连续偏导数 ②F(x0,0,20)=0 ③F(x,0,0)≠0 则方程F(x,y,)=0在点(xo,yo)某一邻域内可唯一确 定一个单值连续函数z=f(x,),满足20=∫(x0,y0), 并有连续偏导数 Oz Fx 6x F F 定理证明从略，仅就求导公式推导如下： 8 下页返回结束

定理2 . 若函数 F(x, y,z) z y z x F F y z F F x z = −   = −   , 的某邻域内具有连续偏导数 , 则方程 在点 并有连续偏导数 定一个单值连续函数 z = f (x , y) , 定理证明从略, 仅就求导公式推导如下: 满足 ( , , ) 0 F x0 y0 z0 = ( , , ) 0 Fz x0 y0 z0  ① 在点 满足: ② ③ 某一邻域内可唯一确 机动 目录 上页 下页 返回 结束

设z=f(x,y)是方程F(x,y)=0所确定的隐函数，则 F(x,y,f(x,y)≡0 两边对x求偏导 Fx+F ∂z 三0 在(xoyo,20)的某邻域内F2≠0 同样可得

F(x, y , f (x , y ) )  0 两边对 x 求偏导 Fx z x F F x z = −   z y F F y z = −   同样可得 则 + Fz x z    0 机动 目录 上页 下页 返回 结束