《高等数学》课程教学资源（PPT课件）Ⅱ_D12_2数项级数及审敛法

第之节 第十一章 常数项级数的审敛法 一、正项级数及其审敛法 二、交错级数及其审敛法 三、绝对收敛与条件收敛 Ooo⊙@⑧

二、交错级数及其审敛法 三、绝对收敛与条件收敛 第二节 一、正项级数及其审敛法 常数项级数的审敛法 机动 目录 上页 下页 返回 结束 第十一章

、 正项级数及其审敛法 00 若4n≥0，则称∑4m为正项级数 n= 定理1.正项级数 ∑4n收敛二部分和序列S n=l (n=1,2,.)有界 证：“>” 若∑4n收敛，则{Sn}收敛，故有界 n=1 .un≥0，.部分和数列{Sn}单调递增 又已知{Sn}有界，故{Sn}收敛，从而∑4n也收敛 n=1 OoO⊙①⑧

一、正项级数及其审敛法 若  0, n u   n=1 un 定理 1. 正项级数 收敛 部分和序列 有界 . 若 收敛 , ∴部分和数列 又已知 有界, 故 从而 故有界. 则称 为正项级数 . 单调递增, 收敛 , 也收敛. 证: “ ” “ ” 机动 目录 上页 下页 返回 结束

定理2（比较审敛法） 设 是两个正项级数， 且有Wn≤ym(n=1,2,.).则 (1①)若级数 ”收敛， 则级数 也收敛； =1 =1 0 ● (2)若级数 ∑发散，则级数 y也发散. 1=1 证： （1)设级数yn收敛于c, 则级数un部分和 Sn=41+42++4n≤y1+V2+.+Vm≤g(n=1,2,.) 由定理1可知，级数 ∑也收敛. n= (2)与(1)等价

定理2 (比较审敛法) 设 且有 (1) 若级数 则级数 (2) 若级数 则级数 证: 则 收敛 , 也收敛 ; 发散 , 也发散 . （1）设级数vn收敛于σ, （2）与（1）等价. 是两个正项级数, 则级数un部分和 由定理 1 可知, 级数 也收敛

0 0 推论设 是两个正项级数，且存在 1=1 1=1 N∈Z,对-切n>N,有4n≤kyn(常数k>0), 则有 0 (1)若级数 收敛， 则级数 也收敛； 0 (2)若级数 ∑.发散， 则级数 ". 也发散

推论 设 且存在 对一切 有 (1) 若级数 则级数 (2) 若级数 则级数 则有 收敛 , 也收敛 ; 发散 , 也发散 . 是两个正项级数, ( 常数 k > 0 )

练习1.判别级数的敛散性 1 )之mD四2吻习 a>0) n=1 1+a4 解：(1)：ln(n+l)1时，. 1 1+a" 故此时原级数收敛 当0<a<l时，lm， n-1+an =1≠0故此时原级数发散 当“=时，原级数为 故此时原级数发散 OOo⊙@⑧

练习1. 判别级数的敛散性: 解: (1)   =1 1 n n 发散 , 故原级数发散 . (2) 故此时原级数收敛 . 机动 目录 上页 下页 返回 结束   =1 3 1 n n 收敛 故原级数收敛 . (3) 故此时原级数发散 .   =1 2 1 n 故此时原级数发散

例1.讨论p级数1+ 30 h2+.(常数p>0) 的收敛性 解：1)若p≤1，【 因为对一切n∈Z, 1、1 n 而调和级数 发散，由比较审敛法可知p级数 发散

例1. 讨论 p 级数 1 1 1 1 2 3 p p p n + + + + + (常数 p > 0) 的收敛性. 解: 1) 若 p  1, 因为对一切 而调和级数 1 1 n n  =  由比较审敛法可知 p 级数 1 n  发散 . 发散

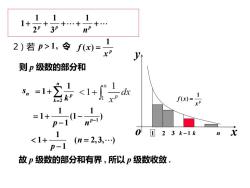
11 1 1+ 2p+30 . 2)若p>1,令f)= y 则p级数的部分和 1 =1+ hP-T 0□23k-1k <1+ p-1 (n=2,3,. 故p级数的部分和有界，所以p级数收敛

p  1, 令 1 1 1 1 (1 ) 1 p p n − = + − − 则 p 级数的部分和 n s 2 1 1 n p k= k = + 故 p 级数的部分和有界 , 所以 p 级数收敛 . 1 1 ( 2,3, ) 1 n p  + = − 2）若 1 1 1 1 2 3 p p p n + + + + + 1 ( ) p f x x = 1 n 1 ( ) p f x x = 2 3 k − 1 k x y o

调和级数与p级数是两个常用的比较级数 若存在N∈Z+,对一切n≥W, ()4≥则24n发散： n=l ②(>.则上%收数 n=1 O©O⊙⑨⑧

调和级数与 p 级数是两个常用的比较级数. 若存在 , + N  Z 对一切 n  N , 机动 目录 上页 下页 返回 结束

例2.证明级数 ∑ √n(n+) 发散 1 证：因为 n(n+1) Vn+1)2 n+1 (n=1,2,.) 而级数 发散 k=2 根据比较审敛法可知，所给级数发散 1 例3.判断级数∑ 的敛散性 台n(n+1)(n+2) 解：因为 ma+2月 的领数收数 根据比较审敛法可知，所给级数收敛 OOo⊙@⑧

证明级数 发散 . 证: 因为 2 ( 1) 1 ( 1) 1 +  n n + n 而级数   = = 2 1 k k 发散 根据比较审敛法可知, 所给级数发散 . 例2. 机动 目录 上页 下页 返回 结束 例3. 判断级数 的敛散性 . 解: 因为 3 1 ( 1)( 2) 1 n n n n  + + 根据比较审敛法可知, 所给级数收敛

例4.若级数∑an与∑bn均收敛，且an≤cn≤bn n=1 n=1 (n=1,2,),证明级数∑cn收敛 n=1 证：：0≤cn-an≤bm-an(n=1,2,),则由题设 ∑(bn-an)收敛>∑(cn-an)收敛 n=l n=1 >∑cn=∑I(cn-an)+an] n=l n=1 00 00 =∑(cn-an)+∑an收敛 n=1 n=l O©O⊙①⑧

例4. 若级数 均收敛 , 且 证明级数 收敛 . 证: n n n n 0  c − a  b − a (n = 1 , 2 , ), 则由题设 ( ) 1 n n n  b − a  = 收敛 ( ) 1 n n n  c − a  = 收敛 [( ) ] 1 n n n n =  c − a + a  = ( ) 1 n n n =  c − a  =   = + n 1 n a 收敛 机动 目录 上页 下页 返回 结束