《高等数学》课程教学资源（PPT课件）Ⅱ_D11_3格林公式

第三节 第十章 格林公式及其应用 格林公式 二、 平面上曲线积分与路径无关的 等价条件 三、二元函数全微分求原函数

第三节 一、格林公式 二、平面上曲线积分与路径无关的 等价条件 机动 目录 上页 下页 返回 结束 格林公式及其应用 第十章 三、二元函数全微分求原函数

格林公式 单连通区域（无“洞”区域 区域D分类 多连通区域（有”洞”区域 域D边界L的正向：域的内部靠左 定理1.设区域D是由分段光滑正向曲线L围成，函数 P(x,y),Q(x,y)在D上具有连续一阶偏导数，则有 e+-川g- (格林公式) 或

L D 区域 D 分类 单连通区域 ( 无“洞”区域 ) 多连通区域 ( 有“洞”区域 ) 域 D 边界L 的正向: 域的内部靠左 定理1. 设区域 D 是由分段光滑正向曲线 L 围成, 则有 x y y P x Q P x Q y L D d d d d             −   + = ( 格林公式 ) 函数 在 D 上具有连续一阶偏导数,    = +    D L x y x y P x Q y P Q 或 d d d d 一、 格林公式 机动 目录 上页 下页 返回 结束

证明：1)若D既是X-型区域，又是Y-型区域，且 p1(x)≤y≤p2(x) a≤x≤b 4()≤x≤Ψ2(y) c≤y≤d 则L2syea =∫0y2y以y)dy-Qw1吵，y)d =∫Q(x,yy-JcaQ(x,yd =∫6Qx,Hy+Eac(x,y OC8 定用1 下页返回结束

证明: 1) 若D 既是 X - 型区域 , 又是 Y - 型区域 , 且        a x b x y x D ( ) ( ) : 1  2 则 x y x Q D d d     = d c Q( ( y), y )dy  2   ( )  ( ) 2 1 d y y x x  Q   = CBE Q(x, y)dy  + EAC Q(x, y)dy  − d c Q( ( y), y )dy 1  = d c dy d c y o x E C A B a b D 定理1 目录 上页 下页 返回 结束

即 那b2ddy-,exya 同理可证 ady-Pds ①、 ②两式相加得 0a, 结球

即 同理可证 ① ② ①、②两式相加得: ( )   = +   −   D L x y P x Q y y P x Q d d d d 定理1 目录 上页 下页 返回 结束

2)若D不满足以上条件，则可通过加辅助线将其分割 为有限个上述形式的区域，如图 k三 -∑mPax+Od(D:表示D,的正向边界） =,Pdx+Qdy 证毕 8 定用1 上页 下页返回结束

y o x L 2) 若D不满足以上条件, 则可通过加辅助线将其分割 D1 Dn D2  ( )  =   −   = n k D x y y P x Q k 1 d d ( ) x y y P x Q D d d   −     =  = + n k Dk P x Q y 1 d d  = + L Pdx Qdy 为有限个上述形式的区域 , 如图 ( 表示 的正向边界) Dk Dk  证毕 定理1 目录 上页 下页 返回 结束

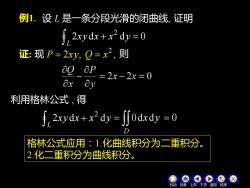
例1.设L是一条分段光滑的闭曲线，证明 f 2xydx+x2dy=0 证：现P=2xy,Q=x2,则 0_P=2x-2x=0 Ox Oy 利用格林公式，得 f2xyd+d=∬0drdy=-0 D 格林公式应用：1.化曲线积分为二重积分。 2.化二重积分为曲线积分

例1. 设 L 是一条分段光滑的闭曲线, 证明 2 d d 0 2 + =  xy x x y L 证: 现 2 , , 2 P = xy Q = x 则 利用格林公式 , 得 xy x x y L 2 d d 2  +  = D 0dx dy = 0 机动 目录 上页 下页 返回 结束 格林公式应用：1.化曲线积分为二重积分。 2.化二重积分为曲线积分

例2：P216题1(2) (答案8 题7(1) (答案：12) 练习：P217题7(2)，题4 例3：P203题3(4) 机动目录上页下页返回结束

例2：P216题1（2） 题7 （1） 机动 目录 上页 下页 返回 结束 (答案：8） (答案：12） 练习：P217题7（2），题4 例3：P203题3（4）

例4.计算∫（x2+3y)dx+(0y2-x)dy,其中L为上半 圆周y=4x-x2从0(0,0)到A(4,0).(补线法) 解：为了使用格林公式，添加辅助线段AO,它与L所围 区域为D,则 原式=+0（2+3)dx+0少2-刘dy (x2+3y)dx+(y2-x)dy =4j川dxdy-4xd 8π+ 64 8 结

y o A x L 例4. 计算 其中L 为上半 从 O (0, 0) 到 A (4, 0).（补线法） 解: 为了使用格林公式, 添加辅助线段 AO, D 它与L 所围 原式 x y x y x y L AO ( 3 ) d ( ) d 2 2 = + + −  +  = D 4 dxdy  − + + − A O (x 3y) d x ( y x) d y 2 2  − 0 4 2 x dx 圆周 区域为D , 则 机动 目录 上页 下页 返回 结束 3 64 = 8 +

练习1设C为沿x2+y2=a2从点(0，a)依逆时针 到点(0，-a)的半圆，计算 dx+[ax+2yln(x+Va2+x2)]dy cva-+x 解：添加辅助线如图，利用格林公式 原式=Jc+c-Jc "(2ylna)dy C8 1打 下页返回结束

 +    − C C C D y o x a − a C 设 C 为沿 x ax y x a x  y a x y C d 2 ln( ) d 2 2 2 2 2 + + + + +  2 2 2 x + y = a 从点 (0,a) 依逆时针 (0,−a) 的半圆, 计算 解: 添加辅助线如图 ,利用格林公式 . 原式 = − − a a (2y ln a) d y    = D 2 2 2 a x y + − d x d y   C 到点 机动 目录 上页 下页 返回 结束 − 0 练习1

刚5计算， 其中L为一无重点且不过原点 的分段光滑正向闭曲线 解： -V P= 则当x2+y2≠0时， 设L所围区域为D, (I).当(0,0)D时，由格林公式知 结

例5. 计算 其中L为一无重点且不过原点 的分段光滑正向闭曲线. 解: 0 , 则当x 2 + y 2  时 设 L 所围区域为D, 当(0,0) D时, 由格林公式知 y o x L 机动 目录 上页 下页 返回 结束 (1)