《高等数学》课程教学资源（PPT课件）Ⅱ_第九章 第四节 多元复合函数的求导法则

第八章第四节多元复合函数的求导法则元复合函数y= f(u), u=@(x)dydy du求导法则dx du dx微分法则dy= f'(u)du= f'(u)p'(x)dx本节内容：多元复合函数求导的链式法则多元复合函数的全微分OOO自录-返回

第四节 一元复合函数 求导法则 本节内容: 一、多元复合函数求导的链式法则 二、多元复合函数的全微分 微分法则 机动 目录 上页 下页 返回 结束 多元复合函数的求导法则 第八章

多元复合函数求导的链式法则定理。若函数u=β(t),v=y(t)在点t可导,z= f(u,v)在点(u,v)处有连续偏导数,则复合函数z= f((t),y (t))在点t可导，且有链式法则7dz oz du.oz ddt ou dt ?v dt证：设t取增量At，则相应中间变量z= f(u,v)有增量^u,由偏导数连续知在点(u,v）处可微，于是azOzAv +o(p) (p = /(△u)? +(△v)?Au+XZ一OvOu目录机动-下页反回结束

一、多元复合函数求导的链式法则 定理. 若函数 z = f (u,v) 处有连续偏导数, 在点 t 可导, t v v z t u u z t z d d d d d d     +   = z 则复合函数 证: 设 t 取增量△t , v v z u u z z     +    = + o (  ) 则相应中间变量 且有链式法则 u v t t 机动 目录 上页 下页 返回 结束 有增量△u , △v ,由偏导数连续知 z = f (u,v) 处可微，于是

OzAyAzozAuo(p)(p = /(Au)? +(△v)2Ou △tAtOv △t△t令△t→0,则有u→0,△v→0dudv△uAvudtdt△t△to(p)o(p)Nu0△tNp(At< 0 时,根式前加"_"号OzOz dydzdu全导数公式，条件可改为Xdt Ou dt'ov dt可微)0000an土

则有u → 0, v → 0, ( 全导数公式 ，条件可改为 可微) t v v z t u u z t z     +     =   t o  + (  ) z u v t t ( ( ) ( ) ) 2 2  = u + v ( )  o  = (△t＜0 时,根式前加“–”号) t v t v t u t u d d , d d →   →   机动 目录 上页 下页 返回 结束 t v v z t u u z t z d d d d d d     +   =

推广：设下面所涉及的函数都可微1)中间变量多于两个的情形.例如，z= f(u,V,w)u=p(t), v= y(t), w=o(t)Oz dyvdzOz du.Oz dwOw dtdt Ou dtOydt= f'o'+ fy'+ f'o'2)中间变量是多元函数的情形.例如z=f(u,v), u=p(x,y), v=y(x,y)ozOz OuazOvfioi + f2yiOxOvaxOu OxazOvazazQu= fi'2 + f2V2Ovayayaydu目泰动结束

推广: 1) 中间变量多于两个的情形. 例如, z = f (u,v,w) , 设下面所涉及的函数都可微 . = t z d d = + +  1 2 3 f f f 2) 中间变量是多元函数的情形.例如, z = f (u,v) , u =  (x, y), v = (x, y) =   x z 11 21 = f   + f   1 2 2 2 = = f   + f     y z z z u v w u v x y x y t t t t u u z d d    t v v z d d    + t w w z d d    + x u u z      x v v z      + y u u z      y v v z      + 机动 目录 上页 下页 返回 结束 u =  (t), v = (t), w = (t)

又如, z= f(x,v), v=(x,y)Z当它们都具有可微条件时，有OzafOvaf4='+f2Vi+axOxovaxXOzafavWaayOvOzaf这里不同注意：S0xOxOzaf表示固定对x求导表示固定y对x求导axOx口诀：分段用乘，分叉用加，单路全导，叉路偏导0000福-F

又如, z = f (x,v), v = (x, y) 当它们都具有可微条件时, 有 x z   1 21 = f  + f   y z   2 2 = f   z = f x x y 注意: 这里 x z   x f   x z   表示固定 y 对 x 求导, x f   表示固定 v 对 x 求导 口诀 : 分段用乘, 分叉用加, 单路全导, 叉路偏导 x f   = 与 不同, v 机动 目录 上页 下页 返回 结束

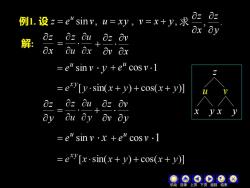
ozoz例i.设z=e"sinv,u=xy，=x+y,求Ox"OyOz uOzOz Ov解：Ox Ou Ox Ov Ox= e" sinv·y +e" cosv.l= e*y[y· sin(x +y)+ cos(x + y)]Oz OuazOz OvVayOu QyOv y=eu sinv·x +eu cosv.l= e*y[x ·sin(x + y)+ cos(x + y))目录反回结束

例1. 设 z e sin v, u xy , v x y , u = = = + , . y z x z     求 解: x z   e v u = sin y z   e v u = sin x v v z      + e v u + cos y v v z      + e v u + cos 1 1 z u v x y x y 机动 目录 上页 下页 返回 结束

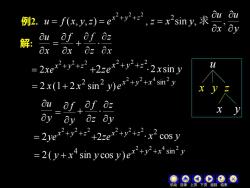
duu+yX,z=x’siny,求例2.u= f(x,y,z)=exox"yafazafdu解：axOx OxOzx?+y?+zu中++2xe2 x sin yze二+y)er?+y?+x+ sin?j1=2x(1+2x~ssinxduOZdafx2ayOZaycos y sinXV+1+x= 2(y+x* sin ycos y)e0000-二-

例2. ( , , ) , sin , 2 2 2 2 u f x y z e z x y x y z = = = + + y u x u     求 , 解: x u   2 2 2 2 x y z xe + + = x y x y x x y e 2 2 4 2 2 2 sin 2 (1 2 sin ) + + = + x y z x y u y u   2 2 2 2 x y z ye + + = x y x y y x y y e 2 2 4 2 4 sin 2 ( sin cos ) + + = + x f   = 2 2 2 2 x y z ze + + + y f   = y z z f      + 2 2 2 2 x y z ze + + +  2 x sin y x cos y 2  机动 目录 上页 下页 返回 结束

例3.设z=uv+sint,u=et,v=cost,求全导数dtOz dydz Oz duoz解：Ov dtatdt Ou dt=vet-usint +cost=et(cost-sin t)+ cost注意：多元抽象复合函数求导在偏微分方程变形与验证解的问题中经常遇到，下列例题有助于掌握这方面问题的求导技巧与常用导数符号dzC练习：设 z=(3x-2y)3x+2y,求：Ox录机动结束XH

例3. 设 z = uv + sin t , . d d t z z u v t t t t z d d t = v e e t t t t = (cos − sin ) + cos t u u z d d    = t z   + u = e t , v = cost , 求全导数 解: + cost 注意：多元抽象复合函数求导在偏微分方程变形与 机动 目录 上页 下页 返回 结束 验证解的问题中经常遇到, 下列例题有助于掌握 问题的求导技巧与常用导数符号. 练习：设 (3 2 ) , , . 3 2 y z x z z x y x y     = − + 求： 这方面

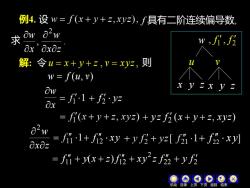
例4.设w=f(x++z,xyz),f具有二阶连续偏导数a?wOw求w,",f2Ox"Ox0z解：令u=x++z,v=xyz,则w= f(u, v)xyzxyow= fi-1 + f2·yzOx= fi(x+ y+z, xyz) + yz f2(x+ y+z, xyz)W= fi·1+ fi2·xy + y f2+yz[ f2i-1+ f22·xy]OxOz= fi1 + y(x+ z)fi2 + xyz f22 + y f2000---F

为简便起见 , 引入记号 , , 2 1 12 u v f f u f f     =    = 例4. 设 f 具有二阶连续偏导数, 求 , . 2 x z w x w      解: 令 u = x + y + z , v = xyz, x w   w u v x y z x y z w = f (u, v) + f   yz 2 ( , ) 2 + y z f  x + y + z xyz 则 x z w    2 22 2 2 11 12 = f  + y(x + z) f  + xy z f  + y f  + f   xy 12 + f   x y 221 2 , f  , f  机动 目录 上页 下页 返回 结束

练习1：P85题8(2)练习2：P85题12（3）P85题8(2)u=duaxouayouaz目录反回结束

P85 题8(2) =   x u 1 f  1 1 f y =  =   y u 1 f  2 + f  =   z u 2 f  2 1 2 1 f z f y x = − +  2 2 f z y = −  机动 目录 上页 下页 返回 结束 练习1：P85 题8(2) 练习2：P85题12（3）